Caccioppoli sets, Part II

After the general introduction to the theory of Caccioppoli sets that was presented in the previous post. I will now sketch some elements of the theory that was developed in our works:

Besov class via heat semigroup on Dirichlet spaces I: Sobolev type inequalities
Besov class via heat semigroup on Dirichlet spaces II: BV functions and Gaussian heat kernel estimates
Besov class via heat semigroup on Dirichlet spaces III: BV functions and sub-Gaussian heat kernel estimates

Dirichlet spaces

Let $X$ be a good measurable space (like a Polish space) equipped with a $\sigma$ -finite measure $\mu$ . Let $(\mathcal{E},\mathcal{F}=\mathbf{dom}(\mathcal{E}))$ be a densely defined closed symmetric form on $L^2(X,\mu)$ . A function $v$ on $X$ is called a normal contraction of the function $u$ if for almost every $x,y \in X$
$| v(x)-v(y)| \le |u(x) -u(y)| \text{ and } |v(x)| \le |u(x)|.$
The form $\mathcal{E}$ is called a Dirichlet form if it is Markovian, that is, has the property that if $u \in \mathcal{F}$ and $v$ is a normal contraction of $u$ then $v \in \mathcal{F}$ and $\mathcal{E}(v,v) \le \mathcal{E} (u,u)$ .

Heat semigroup

Let $\{P_{t}\}_{t\in[0,\infty)}$ denote the self-adjoint heat semigroup on $L^2(X,\mu)$ associated with the Dirichlet space $(X,\mu,\mathcal{E},\mathcal{F})$ :

$\mathcal{E}(f,f)=\lim_{t\to 0^+}\frac{1}{t}\langle (I-P_t)f,f\rangle.$

As is well-known, $P_t: L^2(X,\mu) \cap L^p (X,\mu) \to L^p (X,\mu)$ , $1 \le p \le \infty$ , can be extended into a contraction semigroup $P_t : L^p (X,\mu) \to L^p (X,\mu)$ .

We always assume $P_t1=1$ .

BV space

For $\alpha >0$ , consider the $L^1$ Besov type space
$\mathbf{B}^{1,\alpha}(\mathcal{E})=\left\{ f \in L^1(X,\mu), \limsup_{t\to 0} \frac{1}{t^\alpha} \int_X P_t ( | f - f(y)|) d\mu(y) <+\infty \right\}$ and $\alpha^\#_1(\mathcal{E})=\sup \{ \alpha >0\, :\, \mathbf{B}^{1,\alpha}(\mathcal{E}) \text{ contains non a.e. constant functions} \}.$

Definition: The space of bounded variation functions associated to the Dirichlet form $\mathcal{E}$ is defined as $BV(\mathcal{E})=\mathbf{B}^{1,\alpha^\#}(\mathcal{E})$ . For $f \in BV(\mathcal{E})$ , one defines its variation as
$\mathbf{Var}_\mathcal{E} (f)=\liminf_{t\to 0} \frac{1}{t^\alpha} \int_X P_t ( | f - f(y)|) d\mu(y)$
A set $E \subset X$ is called a $\mathcal{E}$ -Caccioppoli set if $1_E \in BV(\mathcal{E})$ . In that case, its $\mathcal{E}$ -perimeter is defined as $P_\mathcal{E}(E)=\mathbf{Var}_\mathcal{E} (1_E)$ .

Examples

Example 1: Euclidean space

The following can be deduced from M. Miranda Jr, D. Pallara, F. Paronetto, M. Preunkert, 2007. Assume that $\mathcal{E}$ is the standard Dirichlet form on $\mathbb{R}^n$ ,
$\mathcal{E}(f,f)=\int_{\mathbb{R}^n} \| \nabla f \|^2 \, dx, \quad f \in W^{1,2}(\mathbb{R}^n),$
then $\alpha^\#_1(\mathcal{E})=\frac{1}{2}$ , $BV(\mathcal{E})=\mathbf{BV}(\mathbb{R}^n)$ and for $f \in BV(\mathcal{E})$ , $\mathbf{Var}_\mathcal{E} (f)=\frac{2}{\sqrt{\pi}} \| Df \| (\mathbb{R}^n)$ .

Example 2: Sierpinski triangle

Sierpinski triangle

Consider on the Sierpinski triangle $SG$ the Dirichlet form
$\mathcal{E}(f) \simeq \limsup_{r\to 0^+}\frac{1}{r^{d_W}}\int_{SG} \int_{B(x,r)}\frac{|f(y)-f(x)|^2}{ \mu(B(x,r))}\, d\mu(y)\, d\mu(x)$
where $d_W$ is the walk dimension of the Sierpinski triangle.

Then $\alpha^\#_1(\mathcal{E})=\frac{d_H}{d_W}$ , where $d_H$ is the Hausdorff dimension of the Sierpinski triangle and
$\mathbf{Var}_\mathcal{E} (f) \simeq \liminf_{r\to 0^+}\int_{SG} \int_{B(x,r)}\frac{|f(y)-f(x)|}{r^{d_H} \mu(B(x,r))}\, d\mu(y)\, d\mu(x)$
A set $E \subset SG$ is a $\mathcal{E}$ -Caccioppoli set if its boundary is finite.

Example 3: Product of Sierpinski triangles

The space $BV$ behaves nicely with respect to tensorization. Consider the product Dirichlet space $(SG^n, \mathcal{E}^{\otimes n}, \mu^{\otimes n})$ .
Then $\alpha^\#_1(\mathcal{E}^{\otimes n})=\frac{d_H(SG)}{d_W(SG)}$ and
$\mathbf{Var}_{\mathcal{E}^{\otimes n}} (f) \simeq \liminf_{r\to 0^+}\int_{SG^n} \int_{B(x,r)}\frac{|f(y)-f(x)|}{r^{d_H(SG)} \mu(B(x,r))}\, d\mu^{\otimes n}(y)\, d\mu^{\otimes n}(x)$
Therefore, $\mathcal{E}^{\otimes n}$ -Caccioppoli sets have Hausdorff co-dimension $d_H(SG)$ .

Example 4: Riemannian manifolds

Assume that $\mathcal{E}$ is the standard Dirichlet form on a complete Riemannian manifold $\mathbb{M}$ with Ricci curvature bounded from below
$\mathcal{E}(f,f)=\int_{\mathbb{M}} \| \nabla f \|^2 \, dx, \quad f \in W^{1,2}(\mathbb{M})$ , then $\alpha^\#_1(\mathcal{E})=\frac{1}{2}$ , $BV(\mathcal{E})=\mathbf{BV}(\mathbb{M})$ and for $f \in BV(\mathcal{E})$ ,
$\mathbf{Var}_\mathcal{E} (f) \simeq \| Df \| (\mathbb{M}).$

In the case of Riemannian manifolds, the space $\mathbf{BV}(\mathbb{M})$ and the associated notion of variation $\| Df \| (\mathbb{M})$ we are using are for instance presented in the paper: Heat semigroup and functions of bounded variation on Riemannian manifolds by M. Miranda Jr, D. Pallara, F. Paronetto & M. Preunkert.

Example 5: Carnot groups

The following can be deduced from the paper Two Characterization of BV Functions on Carnot Groups via the Heat Semigroup by M. Bramanti, M. Miranda Jr. & D. Pallara. Assume that $\mathcal{E}$ is the Dirichlet form associated to a sub-Laplacian on a Carnot group $\mathbb{G}$
$\mathcal{E}(f,f)=\int_{\mathbb{G}} \| \nabla_{\mathcal H} f \|^2 \, dx, \quad f \in W_{\mathcal H}^{1,2}(\mathbb{G}),$
then $\alpha^\#_1(\mathcal{E})=\frac{1}{2}$ , $BV(\mathcal E)=\mathbf{BV}_\mathcal{H} (\mathbb{G})$ and for $f \in BV(\mathcal{E})$ ,
$\mathbf{Var}_\mathcal{E} (f) =\int_\mathbb{G} \sigma (x) d D_{\mathcal H}f (x) \simeq \| D_{\mathcal H}f \| (\mathbb{G}).$

Locality in time property

Let $(X,\mu,\mathcal{E},\mathcal{F})$ be a Dirichlet space. We consider the following property:
$\mathcal{P}_\infty: \quad \quad \quad \quad \mathbf{Var}_{\mathcal{E}} (f) \simeq \sup_{t >0} \frac{1}{t^{\alpha^\#_1(\mathcal{E})}} \int_X P_t ( | f - f(y)|) d\mu(y)$

Theorem: (Weak Bakry-Emery estimates I)
Let $(X,\mu,\mathcal{E},\mathcal{F})$ be a strictly local metric Dirichlet space that is locally doubling and that locally supports a 2-Poincar\’e inequality on balls.
If there exists a constant $C>0$ such that
$\| |\nabla P_t f | \|_{L^\infty (X,\mu)} \le \frac{C}{\sqrt{t}} \| f \|_{L^\infty (X,\mu)}, \quad t >0.$
Then, $\alpha^\#_1(\mathcal{E})=\frac{1}{2}$ and $\mathcal{P}_\infty$ is satisfied.
The theorem applies to $RCD(0,\infty)$ spaces, Carnot groups and large classes of sub-Riemannian manifolds with non-negative Ricci curvature in the sense of Baudoin-Garofalo.

Theorem: (Weak Bakry-Emery estimates II)
Let $(X,\mu,\mathcal{E},\mathcal{F})$ be a metric Dirichlet space with a heat kernel admitting sub-Gaussian estimates. If there exists a constant $C>0$ such that
$| P_t f(x)-P_tf(y)| \le C \frac{d(x,y)^\kappa}{t^{\kappa/d_W}} \| f \|_{L^\infty (X,\mu)}, \quad t >0.$
where $\kappa=d_W (1-\alpha^\#_1(\mathcal{E}))$ then $\mathcal{P}_\infty$ is satisfied.
This applies to the unbounded Sierpinski triangle and their products and large classes of fractals or products of fractals. This is however a conjecture on the Sierpinski carpet.

Sierpinski carpet

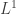$L^1$ -Sobolev inequality and isoperimetric inequality

Let $(X,\mu,\mathcal{E},\mathcal{F})$ be a Dirichlet space.

Theorem: Assume $\mathcal{P}_\infty$ is satisfied and that $P_t$ admits a measurable heat kernel $p_t(x,y)$ satisfying, for some $C>0$ and $\beta >0$ ,
$p_{t}(x,y)\leq C t^{-\beta}, \quad t>0.$
Then, if $0<\alpha^\#_1(\mathcal{E}) <\beta$ , there exists a constant $C>0$ such that for every $f \in BV(\mathcal{E})$ ,
$\| f \|_{L^q(X,\mu)} \le C\mathbf{Var}_{\mathcal{E}} (f),$
where $q=\frac{\beta}{ \beta- \alpha^\#_1(\mathcal{E})}$ .

Under the assumptions of this theorem, one therefore obtains the following general isoperimetric inequality for Caccioppoli sets in Dirichlet spaces
$\mu(E)^{\frac{ \beta- \alpha^\#_1(\mathcal{E})}{\beta}}\le C P_\mathcal{E} (E).$

It generalizes the isoperimetric inequality which was known in Riemannian manifolds or Carnot groups (due to N. Varopoulos) but also applies to new situations like fractals.