Research and Lecture notes

Lecture 5. Rough paths. Fall 2017

Posted on September 13, 2017 by Fabrice Baudoin

In this lecture we define the Young‘s integral $\int y dx$ when $x \in C^{p-var} ([0,T], \mathbb{R}^d)$ and $y \in C^{q-var} ([0,T], \mathbb{R}^{e \times d})$ with $\frac{1}{p}+\frac{1}{q} >1$ . The cornerstone is the following Young-Loeve estimate.

Theorem: Let $x \in C^{1-var} ([0,T], \mathbb{R}^d)$ and $y \in C^{1-var} ([0,T], \mathbb{R}^{e \times d})$ . Consider now $p,q \ge 1$ with $\theta=\frac{1}{p}+\frac{1}{q} > 1$ . The following estimate holds: for $0 \le s \le t \le T$ ,
$\left\| \int_s^t y(u)dx(u)-y(s)(x(t)-x(s)) \right\| \le \frac{1}{1-2^{1-\theta} }\| x \|_{p-var; [s,t]} \| y \|_{q-var; [s,t]}.$

Proof: For $0 \le s \le t \le T$ , let us define
$\Gamma_{s,t} =\int_s^t y(u)dx(u) -y(s)(x(t)-x(s)) .$
We have for $s < t < u$ ,
$\Gamma_{s,u}-\Gamma_{s,t}-\Gamma_{t,u} =-y(s)(x(u)-x(s))+y(s)(x(t)-x(s))+y(t)(x(u)-x(t))= (y(s)-y(t))(x(t)-x(u)).$
As a consequence, we get
$\| \Gamma_{s,u}\|\le \| \Gamma_{s,t} \|+\| \Gamma_{t,u}\| +\| x \|_{p-var; [s,t]} \| y \|_{q-var; [t,u]}.$
Let now $\omega(s,t)=\| x \|^{1/\theta}_{p-var; [s,t]} \| y \|^{1/\theta}_{q-var; [s,t]}$ . We claim that $\omega$ is a control. The continuity and the vanishing on the diagonal are obvious to check, so we just need to justify the superadditivity. Let $s < t < u$ , we have from Holder’s inequality,
$\omega(s,t)+\omega(t,u)$
$=\| x \|^{1/\theta}_{p-var; [s,t]} \| y \|^{1/\theta}_{q-var; [s,t]}+\| x \|^{1/\theta}_{p-var; [t,u]} \| y \|^{1/\theta}_{q-var; [t,u]}$
$\le (\| x \|^{p}_{p-var; [s,t]} + \| x \|^{p}_{p-var; [t,u]})^{\frac{1}{p\theta}}(\| y \|^{q}_{q-var; [s,t]} + \| y \|^{q}_{q-var; [t,u]})^{\frac{1}{q\theta}}$
$\le \| x \|^{1/\theta}_{p-var; [s,u]} \| y \|^{1/\theta}_{q-var; [s,u]}=\omega(s,u).$
We have then
$\| \Gamma_{s,u}\|\le \| \Gamma_{s,t} \|+\| \Gamma_{t,u}\| +\omega(s,u)^\theta.$
For $\varepsilon > 0$ , consider then the control
$\omega_\varepsilon (s,t)= \omega(s,t) +\varepsilon ( \| x \|_{1-var; [s,t]} + \| y \|_{1-var; [s,t]}).$
Define now
$\Psi(r)= \sup_{s,u, \omega_\varepsilon (s,u)\le r} \| \Gamma_{s,u}\|.$
If $s,u$ is such that $\omega_\varepsilon (s,u) \le r$ , we can find a $t$ such that $\omega_\varepsilon(s,t) \le \frac{1}{2} \omega_\varepsilon(s,u)$ , $\omega_\varepsilon(t,u) \le \frac{1}{2} \omega_\varepsilon(s,u)$ . Indeed, the continuity of $\omega_\varepsilon$ forces the existence of a $t$ such that $\omega_\varepsilon(s,t)=\omega_\varepsilon(t,u)$ . We obtain therefore
$\| \Gamma_{s,u}\|\le 2 \Psi(r/2) + r^\theta,$
which implies by maximization,
$\Psi(r)\le 2 \Psi(r/2) + r^\theta.$
By iterating $n$ times this inequality, we obtain
$\Psi(r)$
$\le 2^n \Psi\left(\frac{r}{2^n} \right) +\sum_{k=0}^{n-1} 2^{k(1-\theta)} r^\theta$
$\le 2^n \Psi\left(\frac{r}{2^n} \right) + \frac{1}{1-2^{1-\theta}} r^\theta.$
It is now clear that:
$\| \Gamma_{s,t} \|$
$\le \left\|\int_s^t (y(u)-y(s))dx(u) \right\|$
$\le \| x \|_{1-var; [s,t]} \| y-y(s) \|_{\infty; [s,t]}$
$\le ( \| x \|_{1-var; [s,t]} + \| y \|_{1-var; [s,t]})^2$
$\le \frac{1}{\varepsilon^2} \omega_\varepsilon (s,t)^2,$

Since
$\lim_{n \to \infty} 2^n \Psi\left(\frac{r}{2^n} \right) =0.$
We conclude
$\Psi(r) \le \frac{1}{1-2^{1-\theta}} r^\theta$
and thus
$\| \Gamma_{s,u}\| \le \frac{1}{1-2^{1-\theta}} \omega_\varepsilon(s,u) ^\theta$
Sending $\varepsilon \to 0$ , finishes the proof $\square$

It is remarkable that the Young-Loeve estimate only involves $\| x \|_{p-var; [s,t]}$ and $\| y \|_{q-var; [s,t]}$ . As a consequence, we obtain the following result whose proof is let to the reader:

Proposition: Let $x \in C^{p-var} ([0,T], \mathbb{R}^d)$ and $y \in C^{q-var} ([0,T], \mathbb{R}^{e \times d})$ with $\theta=\frac{1}{p}+\frac{1}{q} >1$ . Let us assume that there exists a sequence $x^n \in C^{1-var} ([0,T], \mathbb{R}^d)$ such that $x^n \to x$ in $C^{p-var} ([0,T], \mathbb{R}^d)$ and a sequence $y^n \in C^{1-var} ([0,T], \mathbb{R}^{e \times d})$ such that $y^n \to x$ in $C^{q-var} ([0,T], \mathbb{R}^d)$ , then for every $s < t$ , $\int_s^t y^n(u)dx^n(u)$ converges to a limit that we call the Young’s integral of $y$ against $x$ on the interval $[s,t]$ and denote $\int_s^t y(u)dx(u)$ .
The integral $\int_s^t y(u)dx(u)$ does not depend of the sequences $x^n$ and $y^n$ and the following estimate holds: for $0 \le s \le t \le T$ ,
$\left\| \int_s^t y(u)dx(u)-y(s)(x(t)-x(s)) \right\| \le \frac{1}{1-2^{1-\theta} }\| x \|_{p-var; [s,t]} \| y \|_{q-var; [s,t]}.$

The closure of $C^{1-var} ([0,T], \mathbb{R}^d)$ in $C^{p-var} ([0,T], \mathbb{R}^d)$ is $C^{0, p-var} ([0,T], \mathbb{R}^d)$ and we know that $C^{p+\varepsilon-var} ([0,T], \mathbb{R}^d) \subset C^{0, p-var} ([0,T], \mathbb{R}^d)$ . It is therefore obvious to extend the Young’s integral for every $x \in C^{p-var} ([0,T], \mathbb{R}^d)$ and $y \in C^{q-var} ([0,T], \mathbb{R}^{e \times d})$ with $\theta=\frac{1}{p}+\frac{1}{q} >1$ and the Young-Loeve estimate still holds
$\left\| \int_s^t y(u)dx(u)-y(s)(x(t)-x(s)) \right\| \le \frac{1}{1-2^{1-\theta} }\| x \|_{p-var; [s,t]} \| y \|_{q-var; [s,t]}.$
From this estimate, we easily see that for $x \in C^{p-var} ([0,T], \mathbb{R}^d)$ and $y \in C^{p-var} ([0,T], \mathbb{R}^{e \times d})$ with $\frac{1}{p}+\frac{1}{q} > 1$ the sequence of Riemann sums
$\sum_{k=0}^{n-1} y(t_i)( x_{t_{i+1}}-x_{t_i})$
will converge to $\int_s^t y(u)dx(u)$ when the mesh of the subdivision goes to 0. We record for later use the following estimate on the Young’s integral, which is also an easy consequence of the Young-Loeve estimate (see Theorem 6.8 in the book for further details).

Proposition: Let $x \in C^{p-var} ([0,T], \mathbb{R}^d)$ and $y \in C^{q-var} ([0,T], \mathbb{R}^{e \times d})$ with $\frac{1}{p}+\frac{1}{q} > 1$ . The integral path $t \to \int_0^t y(u)dx(u)$ is continuous with a finite $p$ -variation and we have
$\left\|\int_0^\cdot y(u) dx(u) \right\|_{p-var, [s,t] }$
$\le C \| x \|_{p-var; [s,t]} \left( \| y \|_{q-var; [s,t]} + \| y \|_{\infty; [s,t]} \right)$
$\le 2C \| x \|_{p-var; [s,t]} \left( \| y \|_{q-var; [s,t]} + \| y(0)\| \right)$

Posted in Rough paths theory | 1 Comment

MA3160. HW2. Due 09/16/2021

Posted on September 8, 2017 by Fabrice Baudoin

Exercise 1. Suppose that A and B are pairwise disjoint events for which P(A) = 0.3 and P(B) = 0.5.

What is the probability that B occurs but A does not?
What is the probability that neither A nor B occurs?

Exercise 2. Forty percent of the students at a certain college are members neither of an academic club nor a Greek organization. Fifty percent are members of an academic club and thirty percent are members of a Greek organization. What is the probability that a randomly chosen student is

member of an academic club or a Greek organization?
member of an academic club and of a Greek organization?

Exercise 3. In a seminar attended by 24 students, what is the probability that at least two of them have the same birthday ?

Honors Exercise: Find the probability of randomly drawing the following poker hands.

A one pair, which consists of two cards of the same rank and three other distinct ranks. (e.g. 22Q59)
A two pair, which consists of two cards of the same rank, two cards of another rank, and another card of yet another rank. (e.g.JJ779)
A three of a kind, which consists of a three cards of the same rank, and two others of distinct rank (e.g. 4449K).
A 􏰄flush, which consists of all 􏰃ve cards of the same suit (e.g. HHHH, SSSS, DDDD, or CCCC).
(E) A full house, which consists of a two pair and a three of a kind (e.g. 88844). (Hint: Note that 88844 is a di􏰂erent hand than a 44488.)

Posted in MA3160 | Leave a comment

Lecture 4. Rough paths. Fall 2017

Posted on September 6, 2017 by Fabrice Baudoin

Our next goal in this course is to define an integral that can be used to integrate rougher paths than bounded variation. As we are going to see, Young’s integration theory allows to define $\int y dx$ as soon as $y$ has finite $q$ -variation and $x$ and has a finite $p$ -variation with $1/p+1/q>1$ . This integral is simply is a limit of Riemann sums as for the Riemann-Stiletjes integral. In this lecture we present some basic properties of the space of continuous paths with a finite $p$ -variation. We present these results for $\mathbb{R}^d$ valued paths but most of the results extend without difficulties to paths valued in metric spaces (see chapter 5 in the book by Friz-Victoir).

Definition. A path $x:[s,t] \to \mathbb{R}^d$ is said to be of finite $p$ -variation, $p > 0$ if the $p$ -variation of $x$ on $[s,t]$ , which is defined as
$\| x \|_{p-var; [s,t]} :=\left( \sup_{ \Pi \in \Delta[s,t]} \sum_{k=0}^{n-1} \| x(t_{k+1}) -x(t_k) \|^p \right)^{1/p},$
is finite. The space of continuous paths $x : [s,t] \to \mathbb{R}^d$ with a finite $p$ -variation will be denoted by $C^{p-var} ([s,t], \mathbb{R}^d)$ .

The notion of $p$ -variation is only interesting when $p \ge 1$ .

Proposition: Let $x:[s,t] \to \mathbb{R}^d$ be a continuous path of finite $p$ -variation with $p < 1$ . Then, $x$ is constant.

Proof: We have for $s \le u \le t$ ,
$\| x(u)-x(s)\|$
$\le ( \max \| x(t_{k+1}) -x(t_k) \|^{1-p} ) \left( \sum_{k=0}^{n-1} \| x(t_{k+1}) -x(t_k) \|^p \right)$
$\le ( \max \| x(t_{k+1}) -x(t_k) \|^{1-p} ) \| x \|^p_{p-var; [s,t]}.$

Since $x$ is continuous, it is also uniformly continuous on $[s,t]$ . By taking a sequence of subdivisions whose mesh tends to 0, we deduce then that
$\| x(u)-x(s)\|=0,$
so that $x$ is constant $\square$
The following proposition is immediate:

Proposition: Let $x:[s,t] \to \mathbb{R}^d$ , be a continuous path. If $p \le p'$ then
$\| x \|_{p'-var; [s,t]} \le \| x \|_{p-var; [s,t]}.$
As a consequence $C^{p-var} ([s,t], \mathbb{R}^d) \subset C^{p'-var} ([s,t], \mathbb{R}^d).$

We remind that a continuous map $\omega: \{ 0 \le s \le t \le T \} \to [0,\infty)$ that vanishes on the diagonal is called a control f if for all $s \le t \le u$ ,
$\omega(s,t)+\omega(t,u) \le \omega (s,u).$

Proposition: Let $x \in C^{p-var} ([0,T], \mathbb{R}^d)$ . Then $\omega(s,t)= \| x \|^p_{p-var; [s,t]}$ is a control such that for every $s \le t$ ,
$\| x(s) -x(t) \| \le \omega(s,t)^{1/p}.$

Proof: It is immediate that
$\| x(s) -x(t) \| \le \omega(s,t)^{1/p},$
so we focus on the proof that $\omega$ is a control. If $\Pi_1 \in \Delta [s,t]$ and $\Pi_2 \in \Delta [t,u]$ , then $\Pi_1 \cup \Pi_2 \in \Delta [s,u]$ . As a consequence, we obtain
$\sup_{ \Pi_1 \in \Delta[s,t]} \sum_{k=0}^{n-1} \| x(t_{k+1}) -x(t_k) \|^p +\sup_{ \Pi_2 \in \Delta[t,u]} \sum_{k=0}^{n-1} \| x(t_{k+1}) -x(t_k) \|^p \le \sup_{ \Pi \in \Delta[s,u]} \sum_{k=0}^{n-1} \| x(t_{k+1}) -x(t_k) \|^p,$
thus
$\| x \|^p_{p-var, [s,t]}+ \| x \|^p_{p-var, [t,u]} \le \| x \|^p_{p-var, [s,u]}.$
The proof of the continuity is left to the reader (see also Proposition 5.8 in the book by Friz-Victoir) $\square$

In the following sense, $\| x \|^p_{p-var; [s,t]}$ is the minimal control of a path $x$ .

Proposition: Let $x \in C^{p-var} ([0,T], \mathbb{R}^d)$ and let $\omega: \{ 0 \le s \le t \le T \} \to [0,\infty)$ be a control such that for $0 \le s \le t \le T$ ,
$\| x(s)-x(t) \| \le C \omega (s,t)^{1/p},$
then
$\| x \|_{p-var; [s,t]} \le C \omega(s,t)^{1/p}.$

Proof: We have
$\| x \|_{p-var; [s,t]}$
$= \left( \sup_{ \Pi \in \Delta[s,t]} \sum_{k=0}^{n-1} \| x(t_{k+1}) -x(t_k) \|^p \right)^{1/p}$
$\le \left( \sup_{ \Pi \in \Delta[s,t]} \sum_{k=0}^{n-1} C^p \omega(t_{k}, t_{k+1}) \right)^{1/p}$
$\le C \omega(s,t)^{1/p}$
$\square$

The next result shows that the set of continuous paths with bounded $p$ -variation is a Banach space.

Theorem: Let $p \ge 1$ . The space $C^{p-var} ([0,T], \mathbb{R}^d)$ endowed with the norm $\| x(0) \|+ \| x \|_{p-var, [0,T]}$ is a Banach space.

Proof: The proof is identical to the case $p=1$ , so we let the careful reader check the details $\square$

Again, the set of smooth paths is not dense in $C^{p-var} ([0,T], \mathbb{R}^d)$ for the $p$ -variation convergence topology. The closure of the set of smooth paths in the $p$ -variation norm shall be denoted by $C^{0,p-var} ([0,T], \mathbb{R}^d)$ . We have the following characterization of paths in $C^{0,p-var} ([0,T], \mathbb{R}^d)$ .

Proposition: Let $p \ge 1$ . $x \in C^{0,p-var} ([0,T], \mathbb{R}^d)$ if and only if
$\lim_{\delta \to 0} \sup_{ \Pi \in \Delta[s,t], | \Pi | \le \delta } \sum_{k=0}^{n-1} \| x(t_{k+1}) -x(t_k) \|^p=0.$

Proof: See Theorem 5.31 in the book by Friz-Victoir $\square$

The following corollary shall often be used in the sequel:

Corollary: If $1 \le p< q$ , then $C^{p-var} ([0,T], \mathbb{R}^d) \subset C^{0,q-var} ([0,T], \mathbb{R}^d)$ .

Proof: Let $\Pi \in \Delta[s,t]$ whose mesh is less than $\delta > 0$ . We have
$\sum_{k=0}^{n-1} \| x(t_{k+1}) -x(t_k) \|^q$
$\le \left( \sum_{k=0}^{n-1} \| x(t_{k+1}) -x(t_k) \|^p\right) \max \| x(t_{k+1}) -x(t_k) \|^{p-q}$
$\le \| x \|^p_{p-var; [s,t]} \max \| x(t_{k+1}) -x(t_k) \|^{p-q}.$
As a consequence, we obtain
$\lim_{\delta \to 0} \sup_{ \Pi \in \Delta[s,t], | \Pi | \le \delta } \sum_{k=0}^{n-1} \| x(t_{k+1}) -x(t_k) \|^q=0$ $\square$

Posted in Rough paths theory | 3 Comments

Lecture 3 Rough paths. Fall 2017

Posted on September 6, 2017 by Fabrice Baudoin

Let $x\in C^{1-var} ([0,T], \mathbb{R}^d)$ and let $V : \mathbb{R}^e \to \mathbb{R}^{e\times d}$ be a Lipschitz continuous map. In order to analyse the solution of the differential equation,
$y(t)=y_0+\int_0^t V(y(s)) dx(s),$
and make the geometry enter into the scene, it is convenient to see $V$ as a collection of vector fields $V=(V_1, \cdots, V_d)$ , where the $V_i$ ‘s are the columns of the matrix $V$ . The differential equation then of course writes
$y(t)=y_0+\sum_{i=1}^d \int_0^t V_i (y(s)) dx^i(s),$

Generally speaking, a vector field $V$ on $\mathbb{R}^{e}$ is a map
$\begin{array}{llll} V: & \mathbb{R}^{e}& \rightarrow & \mathbb{R}^{e} \\ & x & \rightarrow & (v_{1}(x),...,v_{e}(x)). \end{array}$
A vector field $V$ can be seen as a differential operator acting on differentiable functions $f: \mathbb{R}^{e} \rightarrow \mathbb{R}$ as follows:
$Vf(x)=\langle V(x), \nabla f (x) \rangle= \sum_{i=1}^e v_i (x) \frac{\partial f}{\partial x_i}.$
We note that $V$ is a derivation, that is for $f,g \in \mathcal{C}^{1} (\mathbb{R}^e , \mathbb{R} )$ ,
$V(fg)=(Vf)g +f (Vg).$
For this reason we often use the differential notation for vector fields and write:
$V=\sum_{i=1}^d v_i(x) \frac{\partial }{\partial x_i}.$
Using this action of vector fields on functions, the change of variable formula for solutions of differential equations takes a particularly concise form:

Proposition: Let $y$ be a solution of a differential equation that writes
$y(t)=y_0+\sum_{i=1}^d \int_0^t V_i (y(s)) dx^i(s),$
then for any $C^1$ function $f: \mathbb{R}^{e} \rightarrow \mathbb{R}$ ,
$f(y(t))=f(y_0)+\sum_{i=1}^d \int_0^t V_i f (y(s)) dx^i(s).$

Let $V$ be a Lipschitz vector field on $\mathbb{R}^e$ . For any $y_0 \in \mathbb{R}^e$ , the differential equation
$y(t)=y_0+\int_0^t V(y(s)) ds$
has a unique solution $y: \mathbb{R} \to \mathbb{R}^e$ . By time homogeneity of the equation, the flow of this equation satisfies
$\pi ( t_1 , \pi( t_2 ,y_0 ) )=\pi (t_1 +t_2,y_0).$
and therefore $\{ \pi( t, \cdot), t \in \mathbb{R}\}$ is a one parameter group of diffeomorphisms $\mathbb{R}^e \to \mathbb{R}^e$ . This group is generated by $V$ in the sense that for every $y_0 \in \mathbb{R}^e$ ,
$\lim_{t\to 0} \frac{\pi(t,y_0) -y_0}{t}=V(y_0).$
For these reasons, we write $\pi(t,y_0)=e^{tV}(y_0)$ . Let us now assume that $V$ is a $C^1$ Lipschitz vector field on $\mathbb{R}^e$ . If $\phi :\mathbb{R}^e \to \mathbb{R}^e$ is a diffeomorphism, the pull-back $\phi^{\ast}V$ of the vector field $V$ by the map $\phi$ is the vector field defined by the chain rule,
$\phi^{\ast}V (x)=(d \phi^{-1} )_{\phi (x) } \left( V (\phi(x)) \right)$ . In particular, if $V'$ is another $C^1$ Lipschitz vector field on $\mathbb{R}^e$ , then for every $t \in \mathbb{R}$ , we have a vector field $(e^{tV})^{\ast} V'$ . The Lie bracket $[V,V']$ between $V$ and $V'$ is then defined as
$[V,V']=\left( \frac{d}{dt} \right)_{t=0} (e^{tV})^{\ast}V'.$
It is computed that
$[ V, V' ](x)=\sum_{i=1}^e \left( \sum_{j=1}^e v_j (x) \frac{\partial v'_i}{\partial x_j}(x)- v'_j (x) \frac{\partial v_i}{\partial x_j}(x)\right)\frac{\partial}{\partial x_i}.$
Observe that the Lie bracket obviously satisfies $[V,V']=-[V',V]$ and the so-called Jacobi identity that is:
$[V,[V',V'']]+[V',[V'',V]]+[V'',[V,V']]=0.$
What the Lie bracket $[V,V']$ really quantifies is the lack of commutativity of the respective flows generated by $V$ and $V'$ .

Lemma: Let $V,V'$ be two $C^1$ Lipschitz vector fields on $\mathbb{R}^e$ . Then, $[V,V']=0$ if and only if for every $s,t \in \mathbb{R}$ ,
$e^{sV} e^{t V'}=e^{sV+tV'}=e^{t V'} e^{sV}.$

Proof: This is a classical result in differential geometry, so we only give one part the proof. From the very definition of the Lie bracket and the multiplicativity of the flow, we see that $[V,V']=0$ if and only if for every $s \in \mathbb{R}$ , $(e^{sV})^{\ast}V'=V'$ . Now, suppose that $[V,V']=0$ . Let $y$ be the solution of the equation
$y(t)=y_0+\int_0^t V'(y(s)) ds.$
Since $(e^{sV})^{\ast}V'=V'$ , we obtain that $e^{sV} (y(t))$ is also a solution of the equation. By uniqueness of solutions, we obtain that
$e^{sV}(y(t))=e^{tV'} ( e^{sV}(y_0)).$
As a conclusion,
$e^{sV} e^{t V'}=e^{t V'} e^{sV}$
$\square$

If we consider a differential equation
$y(t)=y_0+\sum_{i=1}^d \int_0^t V_i (y(s)) dx^i(s),$
as we will see it throughout this class, the Lie brackets $[V_i,V_j]$ play an important role in understanding the geometry of the set of solutions. The easiest result in that direction is the following:

Proposition: Let $x\in C^{1-var} ([0,T], \mathbb{R}^d)$ and let $V_1,\cdots, V_d$ be $C^1$ Lipschitz vector fields on $\mathbb{R}^e$ . Assume that for every $1 \le i,j \le d$ , $[V_i,V_j]=0$ , then the solution of the differential equation
$y(t)=y_0+\sum_{i=1}^d \int_0^t V_i (y(s)) dx^i(s), \quad 0 \le t \le T,$
can be represented as
$y(t)= \exp \left( \sum_{i=1}^d x^i(t) V_i \right) (y_0).$

Proof: Let
$F(x_1,\cdots,x_n)= \exp \left( \sum_{i=1}^d x_i V_i \right) (y_0).$
Since the flows generated by the $V_i$ ‘s are commuting, we get that
$\frac{\partial F}{\partial x_i}(x)=V_i (F(x)).$
The change of variable formula for bounded variation paths implies then that $F(x^1(t),\cdots,x^n(t))$ is a solution and we conclude by uniqueness $\square$

Posted in Rough paths theory | Leave a comment

Rough paths theory Fall 2017. Lecture 2

Posted on September 3, 2017 by Fabrice Baudoin

In this lecture we establish the basic existence and uniqueness results concerning differential equations driven by bounded variation paths and prove the continuity in the 1-variation topology of the solution of an equation with respect to the driving signal.

Theorem: Let $x\in C^{1-var} ([0,T], \mathbb{R}^d)$ and let $V : \mathbb{R}^e \to \mathbb{R}^{e\times d}$ be a Lipschitz continuous map, that is there exists a constant $K > 0$ such that for every $x,y \in \mathbb{R}^e$ ,
$\| V(x)-V(y) \| \le K \| x-y \|.$
For every $y_0 \in \mathbb{R}^e$ , there is a unique solution to the differential equation:
$y(t)=y_0+\int_0^t V(y(s)) dx(s), \quad 0\le t \le T.$
Moreover $y \in C^{1-var} ([0,T], \mathbb{R}^e)$ .

Proof: The proof is a classical application of the fixed point theorem. Let $0 < \tau \le T$ and consider the map $\Phi$ going from the space of continuous functions $[0,\tau] \to \mathbb{R}^e$ into itself, which is defined by
$\Phi(y)_t =y_0+\int_0^t V(y(s)) dx(s), \quad 0\le t \le \tau.$
By using estimates on Riemann-Stieltjes integrals, we deduce that
$\| \Phi(y^1)-\Phi(y^2) \|_{ \infty, [0,\tau]}$
$\le \| V(y^1)-V(y^2) \|_{ \infty, [0,\tau]} \| x \|_{1-var,[0,\tau]}$
$\le K \| y^1-y^2 \|_{ \infty, [0,\tau]} \| x \|_{1-var,[0,\tau]}$
If $\tau$ is small enough, then $K \| x \|_{1-var,[0,\tau]} < 1$ , which means that $\Phi$ is a contraction that admits a unique fixed point $y$ . This $y$ is the unique solution to the differential equation:
$y(t)=y_0+\int_0^t V(y(s)) dx(s), \quad 0\le t \le \tau.$
By considering then a subdivision
$\{ \tau=\tau_1 < \tau_2 < \cdots < \tau_n=T \}$
such that $K \| x \|_{1-var,[\tau_k,\tau_{k+1}]} < 1$ , we obtain a unique solution to the differential equation:
$y(t)=y_0+\int_0^t V(y(s)) dx(s), \quad 0\le t \le T$
$\square$

The solution of a differential equation is a continuous function of the initial condition, more precisely we have the following estimate:

Proposition: Let $x\in C^{1-var} ([0,T], \mathbb{R}^d)$ and let $V : \mathbb{R}^e \to \mathbb{R}^{e\times d}$ be a Lipschitz continuous map such that for every $x,y \in \mathbb{R}^e$ ,
$\| V(x)-V(y) \| \le K \| x-y \|.$
If $y^1$ and $y^2$ are the solutions of the differential equations:
$y^1(t)=y^1(0)+\int_0^t V(y^1(s)) dx(s), \quad 0\le t \le T,$
and
$y^2(t)=y^2(0)+\int_0^t V(y^2(s)) dx(s), \quad 0\le t \le T,$
then the following estimate holds:
$\| y^1 -y^2 \|_{\infty,[0,T]} \le \| y^1(0) -y^2(0) \| \exp \left( K \| x \|_{1-var,[0,T]} \right).$

Proof: We have
$\| y^1-y^2 \|_{\infty,[0,t]} \le \| y^1(0) -y^2(0) \| +K \int_0^t \| y^1-y^2 \|_{\infty,[0,s]} \| dx(s) \|,$
and conclude by Gronwall’s lemma $\square$

This continuity can be understood in terms of flows. Let $x\in C^{1-var} ([0,T], \mathbb{R}^d)$ and let $V : \mathbb{R}^e \to \mathbb{R}^{e\times d}$ be a Lipschitz map. Denote by $\pi (t,y_0)$ , $0 \le t \le T$ , $y_0 \in \mathbb{R}^e$ , the unique solution of the equation
$y(t)=y_0+\int_0^t V(y(s)) dx(s), \quad 0\le t \le T.$
The previous proposition shows that for a fixed $0 \le t \le T$ , the map $y_0 \to \pi (t,y_0)$ is Lipschitz continuous. The set $\{ \pi (t, \cdot), 0 \le t \le T \}$ is called the flow of the equation.
Under more regularity assumptions on $V$ , the map $y_0 \to \pi (t,y_0)$ is even $C^1$ and the Jacobian map solves a linear equation.

Proposition: Let $x\in C^{1-var} ([0,T], \mathbb{R}^d)$ and let $V : \mathbb{R}^e \to \mathbb{R}^{e\times d}$ be a $C^1$ Lipschitz continuous map. Let $\pi(t,y_0)$ be the flow of the equation
$y(t)=y_0+\int_0^t V(y(s)) dx(s), \quad 0\le t \le T.$
Then for every $0\le t \le T$ , the map $y_0 \to \pi (t,y_0)$ is $C^1$ and the Jacobian $J_t=\frac{\partial \pi(t,y_0)}{\partial y_0}$ is the unique solution of the matrix linear equation
$J_t=Id+ \sum_{i=1}^d\int_0^t DV_i(\pi(s,y_0))J_s dx(s)$ ,
where the $V_i$ ‘s denote the columns of the matrix $V$ .

We finally turn to the important estimate showing that solutions of differential equations are continuous with respect to the driving path in the 1-variation topology

Theorem: Let $x^1,x^2 \in C^{1-var} ([0,T], \mathbb{R}^d)$ and let $V : \mathbb{R}^e \to \mathbb{R}^{e\times d}$ be a Lipschitz and bounded continuous map such that for every $x,y \in \mathbb{R}^e$ ,
$\| V(x)-V(y) \| \le K \| x-y \|.$
If $y^1$ and $y^2$ are the solutions of the differential equations:
$y^1(t)=y(0)+\int_0^t V(y^1(s)) dx^1(s), \quad 0\le t \le T,$
and
$y^2(t)=y(0)+\int_0^t V(y^2(s)) dx^2(s), \quad 0\le t \le T,$
then the following estimate holds:
$\| y^1 -y^2 \|_{1-var,[0,T]} \le \| V \|_\infty \left( 1+ K\| x_1 \|_{1-var,[0,T]} \exp \left( K \| x_1 \|_{1-var,[0,T]} \right) \right) \| x^1 -x^2 \|_{1-var,[0,T]} .$

Proof: We first give an estimate in the supremum topology. It is easily seen that the assumptions imply
$\| y^1 -y^2 \|_{\infty ,[0,t]} \le K \int_0^t \| y^1 -y^2 \|_{\infty ,[0,s]} \| dx^1(s) \| +\| V \|_\infty \| x^1 -x^2 \|_{1-var,[0,T]}.$
From Gronwall’s lemma, we deduce that
$\| y^1 -y^2 \|_{\infty ,[0,T]} \le \| V \|_\infty \exp \left( K \| x \|_{1-var,[0,T]} \right) \| x^1 -x^2 \|_{1-var,[0,T]} .$
Now, we also have for any $0\le s \le t \le T$ ,
$\| y^1(t)-y^2(t)-(y^1(s)-y^2(s))\|\le K \| y^1 -y^2 \|_{\infty ,[0,T]} \| x^1 \|_{1-var,[s,t]} +\| V\|_\infty \| x^1 -x^2 \|_{1-var,[s,t]} .$
This implies,
$\| y^1 -y^2 \|_{1-var,[0,T]} \le K \| y^1 -y^2 \|_{\infty ,[0,T]} \| x^1 \|_{1-var,[0,T]} +\| V\|_\infty \| x^1 -x^2 \|_{1-var,[0,T]}$
and yields the conclusion $\square$

Posted in Rough paths theory | Leave a comment

HW1. MA3160. Due 09/09/2021

Posted on August 31, 2017 by Fabrice Baudoin

Suppose a License plate must consist of a combination of 8 numbers or letters. How many license plates are there if:
1. there can only be letters?
2. the first three places are numbers and the last five are letters?
3. the first four places are numbers and the last four are letters, but there can not be any repetitions in the same license plate?
A school of 60 students has awards for the top math, English, history and science student in the school
1. How many ways can these awards be given if each student can only win one award?
2. How many ways can these awards be given if students can win multiple awards?
An iPhone password can be made up of any 6 digit combination.
1. How many different passwords are possible?
2. How many are possible if all the digits are odd?
Suppose you are organizing your textbooks on a book shelf. You have three chemistry books, 5 math books, 5 history books and 5 English books.
1. How many ways can you order the textbooks if you must have math books first, English books second, chemistry third, and history fourth?
2. How many ways can you order the books if each subject must be ordered together?

Posted in MA3160 | Leave a comment

Rough paths theory Fall 2017. Lecture 1

Posted on August 30, 2017 by Fabrice Baudoin

The first few lectures are essentially reminders of undergraduate real analysis materials. We will cover some aspects of the theory of differential equations driven by continuous paths with bounded variation. The point is to fix some notations that will be used throughout the course and to stress the importance of the topology of convergence in 1-variation if we are interested in stability results for solutions with respect to the driving signal.

If 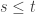$s \le t$ , we will denote by $\Delta [s,t]$ , the set of subdivisions of the interval $[s,t]$ , that is $\Pi \in \Delta [s,t]$ can be written
$\Pi=\left\{ s= t_0 < t_1 < \cdots < t_n =t \right\}.$

Definition: A continuous path $x : [s,t] \to \mathbb{R}^d$ is said to have a bounded variation on $[s,t]$ , if the 1-variation of $x$ on $[s,t]$ , which is defined as
$\| x \|_{1-var; [s,t]} :=\sup_{ \Pi \in \Delta[s,t]} \sum_{k=0}^{n-1} \| x(t_{k+1}) -x(t_k) \|,$
is finite. The space of continuous bounded variation paths $x : [s,t] \to \mathbb{R}^d$ , will be denoted by $C^{1-var} ([s,t], \mathbb{R}^d)$ .

$\| \cdot \|_{1-var; [s,t]}$ is not a norm, because constant functions have a zero 1-variation, but it is obviously a semi-norm. If $x$ is continuously differentiable on $[s,t]$ , it is easily seen (Exercise !) that
$\| x \|_{1-var, [s,t]}=\int_s^t \| x'(s) \| ds.$

Proposition: Let $x \in C^{1-var} ([0,T], \mathbb{R}^d)$ . The function $(s,t)\to \| x \|_{1-var, [s,t]}$ is additive, i.e for $0 \le s \le t \le u \le T$ ,
$\| x \|_{1-var, [s,t]}+ \| x \|_{1-var, [t,u]}= \| x \|_{1-var, [s,u]},$
and controls $x$ in the sense that for $0 \le s \le t \le T$ ,
$\| x(s)-x(t) \| \le \| x \|_{1-var, [s,t]}.$
The function $s \to \| x \|_{1-var, [0,s]}$ is moreover continuous and non decreasing.

Proof: If $\Pi_1 \in \Delta [s,t]$ and $\Pi_2 \in \Delta [t,u]$ , then $\Pi_1 \cup \Pi_2 \in \Delta [s,u]$ . As a consequence, we obtain
$\sup_{ \Pi_1 \in \Delta[s,t]} \sum_{k=0}^{n-1} \| x(t_{k+1}) -x(t_k) \| +\sup_{ \Pi_2 \in \Delta[t,u]} \sum_{k=0}^{n-1} \| x(t_{k+1}) -x(t_k) \| \le \sup_{ \Pi \in \Delta[s,u]} \sum_{k=0}^{n-1} \| x(t_{k+1}) -x(t_k) \|,$
thus
$\| x \|_{1-var, [s,t]}+ \| x \|_{1-var, [t,u]} \le \| x \|_{1-var, [s,u]}.$
Let now $\Pi \in \Delta[s,u]$ :
$\Pi=\left\{ s= t_0 < t_1 < \cdots < t_n =u \right\}.$
Let $k=\max \{ j, t_j \le t\}$ . By the triangle inequality, we have
$\sum_{j=0}^{n-1} \| x(t_{j+1}) -x(t_j) \|$
$\le \sum_{j=0}^{k-1} \| x(t_{j+1}) -x(t_j) \| + \sum_{j=k}^{n-1} \| x(t_{j+1}) -x(t_j) \|$
$\le \| x \|_{1-var, [s,t]}+ \| x \|_{1-var, [t,u]}.$
Taking the $\sup$ of $\Pi \in \Delta[s,u]$ yields
$\| x \|_{1-var, [s,t]}+ \| x \|_{1-var, [t,u]} \ge \| x \|_{1-var, [s,u]},$
which completes the proof. The proof of the continuity and monoticity of $s \to \| x \|_{1-var, [0,s]}$ is let to the reader $\square$

This control of the path by the 1-variation norm is an illustration of the notion of controlled path which is very useful in rough paths theory.

Definition: A map $\omega: \{ 0 \le s \le t \le T \} \to [0,\infty)$ is called superadditive if for all $s \le t \le u$ ,
$\omega(s,t)+\omega(t,u) \le \omega (s,u).$
If, in adition, $\omega$ is continuous and $\omega(t,t)=0$ , we call $\omega$ a control. We say that a path $x:[0,T] \to \mathbb{R}$ is controlled by a control $\omega$ , if there exists a constant $C < 0$ , such that for every $0 \le s \le t \le T$ ,
$\| x(t) -x(s) \| \le C \omega(s,t).$

Obviously, Lipschitz functions have a bounded variation. The converse is of course not true: $t\to \sqrt{t}$ has a bounded variation on $[0,1]$ but is not Lipschitz. However, any continuous path with bounded variation is the reparametrization of a Lipschitz path in the following sense.

Proposition: Let $x \in C^{1-var} ([0,T], \mathbb{R}^d)$ . There exist a Lipschitz function $y:[0,1] \to \mathbb{R}^d$ , and a continuous and non-decreasing function $\phi:[0,T]\to [0,1]$ such that $x=y\circ \phi$ .

Proof: We assume $\| x \|_{1-var, [0,T]} \neq 0$ and consider
$\phi(t)=\frac{ \| x \|_{1-var, [0,t]} }{ \| x \|_{1-var, [0,T]} }.$
It is continuous and non decreasing. There exists a function $y$ such that $x=y\circ \phi$ because $\phi(t_1)=\phi(t_2)$ implies $x(t_1)=x(t_2)$ . We have then, for $s \le t$ ,
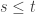$\| y( \phi(t)) -y ( \phi(s)) \|=\| x(t) -x (s) \| \le \| x \|_{1-var, [s,t]} =\| x \|_{1-var, [0,T]} (\phi(t)-\phi(s) )$ $\square$

The next result shows that the set of continuous paths with bounded variation is a Banach space.

Theorem: The space $C^{1-var} ([0,T], \mathbb{R}^d)$ endowed with the norm $\| x(0) \|+ \| x \|_{1-var, [0,T]}$ is a Banach space.

Proof: Let $x^n \in C^{1-var} ([0,T], \mathbb{R}^d)$ be a Cauchy sequence. It is clear that
$\| x^n -x^m \|_\infty \le \| x^n(0)-x^m(0) \|+ \| x^n-x^m \|_{1-var, [0,T]}.$
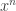Thus, $x^n$ converges uniformly to a continuous path $x :[0,T] \to \mathbb{R}$ . We need to prove that $x$ has a bounded variation. Let
$\Pi=\{ 0=t_0 <t_1 < \cdots <t_n=T \}$
be a a subdivision of $[0,T]$ . There is $m \ge 0$ , such that $\| x - x^m \|_\infty \le \frac{1}{2n}$ , thus
$\sum_{k=0}^{n-1} \|x(t_{k+1})-x(t_k) \|$
$\le \sum_{k=0}^{n-1} \|x(t_{k+1})-x^m(t_{k+1}) \| +\sum_{k=0}^{n-1} \|x^m(t_{k})-x(t_k) \| +\| x^m \|_{1-var,[0,T]}$
$\le 1+\sup_{n} \| x^n \|_{1-var,[0,T]}.$
Thus, we have
$\| x \|_{1-var,[0,T]} \le 1+\sup_{n} \| x^n \|_{1-var,[0,T]} < \infty$
$\square$

For approximations purposes, it is important to observe that the set of smooth paths is not dense in $C^{1-var} ([0,T], \mathbb{R}^d)$ for the 1-variation convergence topology. The closure of the set of smooth paths in the 1-variation norm, which shall be denoted by $C^{0,1-var} ([0,T], \mathbb{R}^d)$ is the set of absolutely continuous paths.

Proposition: Let $x \in C^{1-var} ([0,T], \mathbb{R}^d)$ . Then, $x \in C^{0,1-var} ([0,T], \mathbb{R}^d)$ if and only if there exists $y \in L^1([0,T])$ such that,
$x(t)=x(0)+\int_0^t y(s) ds.$

Proof: First, let us assume that
$x(t)=x(0)+\int_0^t y(s) ds,$
for some $y \in L^1([0,T])$ . Since smooth paths are dense in $L^1([0,T])$ , we can find a sequence $y^n$ in $L^1([0,T])$ such that $\| y-y^n \|_1 \to 0$ . Define then,
$x^n(t)=x(0)+\int_0^t y^n(s) ds.$
We have
$\| x-x^n \|_{1-var,[0,T]}=\| y-y^n \|_1.$
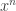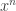This implies that $x \in C^{0,1-var} ([0,T], \mathbb{R}^d)$ . Conversely, if $x \in C^{0,1-var} ([0,T], \mathbb{R}^d)$ , there exists a sequence of smooth paths $x^n$ that converges in the 1-variation topology to $x$ . Each $x^n$ can be written as,
$x^n(t)=x^n(0)+\int_0^t y^n(s) ds.$
We still have
$\| x^m-x^n \|_{1-var,[0,T]}=\| y^m-y^n \|_1,$
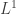so that $y^n$ converges to some $y$ in $L^1$ . It is then clear that
$x(t)=x(0)+\int_0^t y(s) ds$
$\square$

Exercise: Let $x \in C^{1-var} ([0,T], \mathbb{R}^d)$ . Show that $x$ is the limit in 1-variation of piecewise linear interpolations if and only if $x \in C^{0,1-var} ([0,T], \mathbb{R}^d)$ .

Let $y:[0,T] \to \mathbb{R}^{e \times d}$ be a piecewise continuous path and $x \in C^{1-var} ([0,T], \mathbb{R}^d)$ . It is well-known that we can integrate $y$ against $x$ by using the Riemann–Stieltjes integral which is a natural extension of the Riemann integral. The idea is to use the Riemann sums
$\sum_{k=0}^{n-1} y(t_k) (x(t_{k+1})-x(t_k)),$
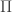where $\Pi=\{ 0 =t_0 < t_1 < \cdots < t_n =T \}$ . It is easy to prove that, when the mesh of the subdivision $\Pi$ goes to 0, the Riemann sums converge to a limit which is independent from the sequence of subdivisions that was chosen. The limit is then denoted $\int_0^T y(t) dx(t)$ and called the Riemann-Stieltjes integral of $y$ against $x$ . Since $x$ has a bounded variation, it is easy to see that, more generally,
$\sum_{k=0}^{n-1} y(\xi_k) (x(t_{k+1})-x(t_k)),$
with $t_k \le \xi_k \le t_{k+1}$ would also converge to $\int_0^T y(t) dx(t)$ . If
$x(t)=x(0)+\int_0^t g(s) ds$
is an absolutely continuous path, then it is not difficult to prove that we have
$\int_0^T y(t) dx(t) =\int_0^T y(t) g(t) dt,$
where the integral on the right hand side is understood in Riemann’s sense.

We have
$\left\| \sum_{k=0}^{n-1} y(t_k) (x(t_{k+1})-x(t_k))\right\|$
$\le \sum_{k=0}^{n-1} \| y(t_k)\| \| (x(t_{k+1})-x(t_k))\|$
$\le \sum_{k=0}^{n-1} \| y(t_k)\| \| (x(t_{k+1})-x(t_k))\|$
$\le \sum_{k=0}^{n-1} \| y(t_k)\| \| x \|_{1-var,[t_k,t_{k+1}]}.$
Thus, by taking the limit when the mesh of the subdivision goes to 0, we obtain the estimate
$\left\| \int_0^T y(t) dx(t) \right\| \le \int_0^T \| y(t) \| \| dx(t) \| \le \| y \|_{\infty, [0,T]} \| x \|_{1-var,[0,T]},$
where $\int_0^T \| y(t) \| \| dx(t) \|$ is the notation for the Riemann-Stieltjes integral of $\| y \|$ against the bounded variation path $l(t)= \| x \|_{1-var,[0,t]}$ . We can also estimate the Riemann-Stieltjes integral in the 1-variation distance. We collect the following estimate for later use:

Proposition: Let $y,y':[0,T] \to \mathbb{R}^{e \times d}$ be a piecewise continuous path and $x,x' \in C^{1-var} ([0,T], \mathbb{R}^d)$ . We have
$\left\| \int_0^{\cdot} y'(t) dx'(t)-\int_0^{\cdot} y(t) dx(t) \right\|_{1-var,[0,T]} \le \| x \|_{1-var,[0,T]} \| y-y' \|_{\infty, [0,T]} + \| y' \|_{\infty, [0,T]} \| x -x'\|_{1-var,[0,T]}.$

The Riemann-Stieltjes satisfies the usual rules of calculus, for instance the integration by parts formula takes the following form
Proposition: Let $y \in C^{1-var} ([0,T], \mathbb{R}^{e \times d} )$ and $x\in C^{1-var} ([0,T], \mathbb{R}^d)$ .
$\int_0^T y(t) dx(t)+\int_0^T dy(t) x(t)=y(T)x(T) -y(0)x(0).$

We also have the following change of variable formula:

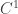Proposition: Let $x\in C^{1-var} ([0,T], \mathbb{R}^d)$ and let $\Phi: \mathbb{R}^d \to \mathbb{R}^e$ be a $C^1$ map. We have
$\Phi (x(T)) =\Phi (x(0)) + \int_0^T \Phi'(x(t)) dx(t).$

Proof: From the mean value theorem
$\Phi (x(T)) -\Phi (x(0))=\sum_{k=0}^{n-1} (\Phi (x(t_{k+1})) -\Phi (x(t_k)))=\sum_{k=0}^{n-1}\Phi'(x_{\xi_k}) (x(t_{k+1}) -x(t_k)),$
with $t_k \le \xi_k \le t_{k+1}$ . The result is then obtained by taking the limit when the mesh of the subdivision goes to 0 $\square$

We finally state a classical analysis lemma, Gronwall’s lemma, which provides a wonderful tool to estimate solutions of differential equations.

Proposition: Let $x \in C^{1-var} ([0,T], \mathbb{R}^d)$ and let $\Phi: [0,T] \to [0,\infty)$ be a bounded measurable function. If,
$\Phi(t) \le A+B\int_0^t \Phi(s) \| d x(s)\|, \quad 0 \le t \le T,$
for some $A,B \ge 0$ , then
$\Phi(t) \le A \exp (B \| x \|_{1-var,[0,t]} )\quad 0 \le t \le T.$

Proof: Iterating the inequality
$\Phi(t) \le A+B\int_0^t \Phi(s) \| d x(s)\|$
$N$ times, we get
$\Phi(t) \le A+\sum_{k=1} ^n AB^{k} \int_0^ t \int_0^{t_1} \cdots \int_0^{t_{k-1}} \| d x(t_k)\| \cdots \| dx(t_1) \| +R_n(t),$
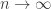where $R_n(t)$ is a remainder term that goes to 0 when $n \to \infty$ . Observing that
$\int_0^ t \int_0^{t_1} \cdots \int_0^{t_{k-1}} \| d x(t_k)\| \cdots \| dx(t_1) \|=\frac{ \| x \|^k_{1-var,[0,t]} }{k!}$
and sending $n$ to $\infty$ finishes the proof $\square$

Posted in Rough paths theory | 3 Comments

MA3160 Probability. Syllabus

Posted on August 28, 2017 by Fabrice Baudoin

The main educational resource for MA3160 is the following webpage: UConn Undergraduate Probability OER.

No book is required and the course will mostly be based on the lecture notes posted here.

There will be two midterm exams and a final exam whose dates will be communicated later.

There will be weekly homework/quiz assignments.

The final grade will be made of 20% first midterm, 20% second midterm, 20% homework/quiz and 40% final exam.

The following topics will be covered.

Introduction: What is probability theory and why do we care ?
Sets
Combinatorics
The probability set-up
Independence
Conditional probability
Random variables
Some discrete distributions
Continuous distributions
Normal distribution
Normal approximation
Some continuous distributions
Multivariate distributions
Expectations
Moment generating functions
Limit laws

Posted in MA3160 | Leave a comment

Rough paths theory. Fall 2017

Posted on August 28, 2017 by Fabrice Baudoin

During the Fall 2017, I will be teaching rough paths theory at the University of Connecticut. The course will be mainly based on those notes and the lectures already posted on this blog in 2013 (when I first taught the class at Purdue University).

Since I first taught the class, the theory of rough paths has found many further applications. A natural and far reaching development is the theory of regularity structures for which Martin Hairer was awarded the Fields medal in 2014 (see my post) . I will therefore update the lectures to reflect those developments. A good introduction to the theory of regularity structures is the book by Peter Friz and Martin Hairer which I will be using as a complement reading.

Posted in Rough paths theory | Leave a comment

MA5311. Take home exam

Posted on April 20, 2017 by Fabrice Baudoin

Exercise 1. Solve Exercise 44 in Chapter 1 of the book.

Exercise 2. Solve Exercise 3 in Chapter 1 of the book.

Exercise 3. Solve Exercise 39 in Chapter 1 of the book.

Exercise 4. The heat kernel on $\mathbb{S}^1$ is given by $p(t,y) =\frac{1}{2\pi}\sum_{m \in \mathbb{Z}} e^{-m^2 t} e^{im y} =\frac{1}{\sqrt{4\pi t}} \sum_{k \in \mathbb{Z}} e^{-\frac{(y -2k\pi)^2}{4t} }$ .

By using the subordination identity $e^{-\tau | \alpha | } =\frac{\tau}{2\sqrt{\pi}} \int_0^{+\infty} \frac{e^{-\frac{\tau^2}{4t}-t \alpha^2}}{t^{3/2}} dt, \quad \tau \neq 0, \alpha \in \mathbb{R},$ show that for $\tau > 0$ , $\frac{1+e^{-2\pi \tau}}{1-e^{-2\pi \tau}} =\frac{1}{2\pi} \sum_{k \in \mathbb{Z}} \frac{2\tau}{\tau^2+n^2}$
The Bernoulli numbers $B_k$ are defined via the series expansion $\frac{x}{e^x -1}=\sum_{k=0}^{+\infty} B_k \frac{x^k}{k!}.$ By using the previous identity show that for $k \in \mathbb{N}$ , $k \neq 0$ , $\sum_{n=1}^{+\infty} \frac{1}{n^{2k}} =(-1)^{k-1} \frac{(2\pi)^{2k} B_{2k} }{2(2k)!}.$

Exercise 5. Show that the heat kernel on the torus $\mathbb{T}^n=\mathbb{R}^n / (2 \pi \mathbb{Z})^n$ is given by $p(t,y) = \frac{1}{(4\pi t)^{n/2}} \sum_{k \in \mathbb{Z}^n} e^{-\frac{\|y+2k\pi\|^2}{4t} }=\frac{1}{(2\pi)^n} \sum_{l\in \mathbb{Z}^n} e^{i l \cdot y -\| l \|^2 t}.$

Posted in Uncategorized | Leave a comment

Research and Lecture notes

Lecture 5. Rough paths. Fall 2017

MA3160. HW2. Due 09/16/2021

Lecture 4. Rough paths. Fall 2017

Lecture 3 Rough paths. Fall 2017

Rough paths theory Fall 2017. Lecture 2

HW1. MA3160. Due 09/09/2021

Rough paths theory Fall 2017. Lecture 1

MA3160 Probability. Syllabus

Rough paths theory. Fall 2017

MA5311. Take home exam

Categories

Blog Stats

Follow Blog via Email

Blogroll

Recent Posts

Meta