In this lecture we define Riemannian structures and corresponding Laplace–Beltrami operators. We first study Riemannian structures on Rn to avoid technicalities in the presentation of the main ideas and then, in a later lecture, will extend our results to the manifold case.
We start with the following basic definition:
Definition: A Riemannian structure on  is a smooth map
is a smooth map  from
from  to the set of symmetric positive matrices.
to the set of symmetric positive matrices.
In other words, a Riemannian structure induces at each point 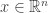 an inner product
an inner product  , and the dependence
, and the dependence  is asked to be smooth.
is asked to be smooth.
A natural way to define Riemannian structures, is to start from a family of smooth vector fields  such that for every
such that for every 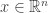 ,
,  is a basis of
is a basis of  . It is then easily seen that there is a unique Riemannian structure on
. It is then easily seen that there is a unique Riemannian structure on  that makes for
that makes for 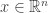 ,
,  an orthonormal basis.
an orthonormal basis.
Conversely, given a Riemannian structure on  , it is possible to find smooth vector fields
, it is possible to find smooth vector fields  on
on  such that for
such that for 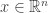 ,
,  an orthonormal basis for this Riemannian structure.
an orthonormal basis for this Riemannian structure.
In this course, we shall mainly deal with such a point of view on Riemannian structures and use as much as possible the language of vector fields. This point of view is not restrictive and will allow more easy extensions to the sub-Riemannian case in a later part of the course.
Let us consider a family of smooth vector fields  such that for every
such that for every 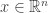 ,
,  is a basis of
is a basis of  . Without loss of generality we may assume that
. Without loss of generality we may assume that  Our goal is to associate to this Riemannian structure a canonical diffusion operator.
Our goal is to associate to this Riemannian structure a canonical diffusion operator.
As a first step, we associate with the vector fields  a natural Borel measure
a natural Borel measure  which is the measure with density
which is the measure with density  with respect to the Lebesgue measure. This is the so-called Riemannian measure. The diffusion operator we want to consider shall be symmetric with respect to this measure.
with respect to the Lebesgue measure. This is the so-called Riemannian measure. The diffusion operator we want to consider shall be symmetric with respect to this measure.
Remark: Let  be another system of smooth vector fields on
be another system of smooth vector fields on  such that for every
such that for every 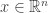 ,
,  is an orthonormal basis with respect to the inner product
is an orthonormal basis with respect to the inner product  . The systems of vector fields
. The systems of vector fields  and
and  are related one to each other through an orthogonal mapping. This implies that
are related one to each other through an orthogonal mapping. This implies that  In other words, the Riemannian measure
In other words, the Riemannian measure  only depends on the Riemannian structure
only depends on the Riemannian structure  .
.
Due to the fact that for every 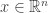 ,
,  is a basis of
is a basis of  , we may find smooth functions
, we may find smooth functions  ‘s on $\mathbb{R}^n$ such that
‘s on $\mathbb{R}^n$ such that ![[V_i,V_j]=\sum_{k=1}^n \omega_{ij}^k V_k.](https://s0.wp.com/latex.php?latex=%5BV_i%2CV_j%5D%3D%5Csum_%7Bk%3D1%7D%5En+%5Comega_%7Bij%7D%5Ek+V_k.&bg=ffffff&fg=333333&s=0&c=20201002) Those functions are called the structure constants of the Riemannian structure. Every relevant geometric quantities may be expressed in terms of these functions. Of course, these functions depend on the choice of the vector fields $V_i$’s and thus are not Riemannian invariants, but several combinations of them, like curvature quantities, are Riemannian invariants.
Those functions are called the structure constants of the Riemannian structure. Every relevant geometric quantities may be expressed in terms of these functions. Of course, these functions depend on the choice of the vector fields $V_i$’s and thus are not Riemannian invariants, but several combinations of them, like curvature quantities, are Riemannian invariants.
The following proposition expresses the formal adjoint with respect to the Lebesgue measure of the vector field  which is seen as an operator acting on the spave of smooth and compactly supported functions.
which is seen as an operator acting on the spave of smooth and compactly supported functions.
Proposition: If  are smooth and compactly supported functions, then we have
are smooth and compactly supported functions, then we have  where
where 
Proof: Let us denote  and
and  We have
We have  We now compute
We now compute  . We then observe that
. We then observe that 
Thus, we obtain


 ,\cdots, V_n(x)\right)](https://s0.wp.com/latex.php?latex=%3D-%5Csum_%7Bk%3D1%7D%5En%5Cmathbf%7Bdet%7D+%5Cleft%28+V_1%28x%29%2C%5Ccdots%2C%5BV_i%2CV_k%5D%28x%29+%2C%5Ccdots%2C+V_n%28x%29%5Cright%29&bg=ffffff&fg=333333&s=0&c=20201002)

 .
. 
With this integration by parts formula in hands we are led to the following natural definition
Definition: The diffusion operator  is called the Laplace-Beltrami operator associated with the Riemannian structure
is called the Laplace-Beltrami operator associated with the Riemannian structure  .
.
The following straightforward properties of  are let as an exercise to the reader:
are let as an exercise to the reader:
 is an elliptic operator;
is an elliptic operator;- The Riemannian measure
 is invariant for
is invariant for  ;
;
- The operator
 is symmetric with respect to
is symmetric with respect to  .
.
Exercise: Let  be another system of smooth vector fields on
be another system of smooth vector fields on  such that for every
such that for every 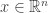 ,
,  is an orthonormal basis with respect to the inner product
is an orthonormal basis with respect to the inner product  . Show that
. Show that  In other words, the Laplace-Beltrami operator is a Riemannian invariant: It only depends on the Riemannian structure
In other words, the Laplace-Beltrami operator is a Riemannian invariant: It only depends on the Riemannian structure  .
.
In order to apply the diffusion semigroup theory developed in the first lectures and construct without ambiguity the semigroup associated to the Laplace-Beltrami operator L, we need to know if L is essentially self-adjoint. Interestingly, this property of essential self-adjointness is clodely related to a metric property of the underlying Riemannian structure: The completeness of the associated distance.
Given an absolutely continuous curve ![\gamma: [0,T] \rightarrow \mathbb{R}^n](https://s0.wp.com/latex.php?latex=%5Cgamma%3A+%5B0%2CT%5D+%5Crightarrow+%5Cmathbb%7BR%7D%5En&bg=ffffff&fg=333333&s=0&c=20201002) , we define its Riemannian length by
, we define its Riemannian length by  If
If  , let us denote by
, let us denote by  the set of absolutely continuous curves
the set of absolutely continuous curves ![\gamma: [0,1] \rightarrow \mathbb{R}^n](https://s0.wp.com/latex.php?latex=%5Cgamma%3A+%5B0%2C1%5D+%5Crightarrow+%5Cmathbb%7BR%7D%5En&bg=ffffff&fg=333333&s=0&c=20201002) such that
such that  The Riemannian distance between
The Riemannian distance between  and
and  is defined by
is defined by  By using reparametrization, we may define the Riemannian distance in a equivalent way by using the notion of sub-unit curve. Let
By using reparametrization, we may define the Riemannian distance in a equivalent way by using the notion of sub-unit curve. Let ![\gamma: [0,T] \to \mathbb{R}^n](https://s0.wp.com/latex.php?latex=%5Cgamma%3A+%5B0%2CT%5D+%5Cto+%5Cmathbb%7BR%7D%5En&bg=ffffff&fg=333333&s=0&c=20201002) be an absolutely continuous curve. Since the vector fields
be an absolutely continuous curve. Since the vector fields  ‘s form a basis of
‘s form a basis of  at each point, we may find continuous functions
at each point, we may find continuous functions ![\alpha_i:[0,T] \to \mathbb{R}^n](https://s0.wp.com/latex.php?latex=%5Calpha_i%3A%5B0%2CT%5D+%5Cto+%5Cmathbb%7BR%7D%5En&bg=ffffff&fg=333333&s=0&c=20201002) such that
such that  The curve
The curve  is then said to be sub-unit if for almost every
is then said to be sub-unit if for almost every ![t \in [0,T]](https://s0.wp.com/latex.php?latex=t+%5Cin+%5B0%2CT%5D&bg=ffffff&fg=333333&s=0&c=20201002) ,
,  . By using reparametrization, it is easily seen that for
. By using reparametrization, it is easily seen that for  ,
, ![d(x,y)=\inf \left\{ T \text{ such that there exists a sub-unit curve } \gamma:[0,T] \to \mathbb{R}^n, \gamma(0)=x, \gamma(1)=y \right\}](https://s0.wp.com/latex.php?latex=d%28x%2Cy%29%3D%5Cinf+%5Cleft%5C%7B+T+%5Ctext%7B+such+that+there+exists+a+sub-unit+curve+%7D+%5Cgamma%3A%5B0%2CT%5D+%5Cto+%5Cmathbb%7BR%7D%5En%2C+%5Cgamma%280%29%3Dx%2C+%5Cgamma%281%29%3Dy+%5Cright%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) .
.
Exercise: Let  . Show that for every
. Show that for every 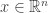 ,
, 
An important fact is that  hence defined is indeed a distance that induces the usual topology of
hence defined is indeed a distance that induces the usual topology of  .
.
Definition: The function  defined above is a distance that induces the usual topology of
defined above is a distance that induces the usual topology of  .
.
Proof: Since any curve can be parametrized backwards and forwards, we have 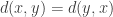 . The triangle inequality is easily proved by using juxtaposition of curves. Plainly
. The triangle inequality is easily proved by using juxtaposition of curves. Plainly  , so it remains to prove that if
, so it remains to prove that if 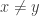 then
then  . Let
. Let  such that
such that 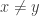 . Let us denote
. Let us denote  . The closed Euclidean ball
. The closed Euclidean ball  is compact, therefore there exist two constants
is compact, therefore there exist two constants  such that for every
such that for every  and
and 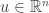 ,
,  Let now
Let now ![\gamma:[0,1]\to \mathbb{R}^n](https://s0.wp.com/latex.php?latex=%5Cgamma%3A%5B0%2C1%5D%5Cto+%5Cmathbb%7BR%7D%5En&bg=ffffff&fg=333333&s=0&c=20201002) be an absolutely continuous curve such that
be an absolutely continuous curve such that  . Let
. Let 
We have







As a consequence, we deduce that  Therefore
Therefore  is indeed a distance. Moreover, it is shown as above that for every
is indeed a distance. Moreover, it is shown as above that for every  , there are constants
, there are constants  such that for every
such that for every  ,
,  This implies that
This implies that  induces the usual topology of
induces the usual topology of 

As shown in the following proposition, the distance  is intrinsically associated to the Laplace-Beltrami operator.
is intrinsically associated to the Laplace-Beltrami operator.
Proposition: For  , we have
, we have 
Proof: Let  . We denote
. We denote  Let
Let ![\gamma: [0,T] \to \mathbb{R}](https://s0.wp.com/latex.php?latex=%5Cgamma%3A+%5B0%2CT%5D+%5Cto+%5Cmathbb%7BR%7D&bg=ffffff&fg=333333&s=0&c=20201002) be a sub-unit curve such that
be a sub-unit curve such that  We can find
We can find ![\alpha_1,\cdots,\alpha_n:[0,T] \to \mathbb{R}^n](https://s0.wp.com/latex.php?latex=%5Calpha_1%2C%5Ccdots%2C%5Calpha_n%3A%5B0%2CT%5D+%5Cto+%5Cmathbb%7BR%7D%5En&bg=ffffff&fg=333333&s=0&c=20201002) such that
such that  and
and  . Let now
. Let now  . From the change of variable formula we have,
. From the change of variable formula we have,  Therefore, from Cauchy-Schwarz inequality,
Therefore, from Cauchy-Schwarz inequality,  As a consequence
As a consequence 
We now prove the converse inequality which is trickier. The idea is to use the function  that satisfies
that satisfies  and
and  . However, giving a precise meaning to
. However, giving a precise meaning to  is not so easy, because it turns out that
is not so easy, because it turns out that  is not differentiable at
is not differentiable at  . It suggests to use an approximation of the identity to regularize
. It suggests to use an approximation of the identity to regularize  and avoid the discussion of this differentiability issue. More precisely, fix
and avoid the discussion of this differentiability issue. More precisely, fix  , and for
, and for  , consider the function
, consider the function  where
where  ,
,  ,
,  ,
,  and
and  ,
,  , has the property that
, has the property that  and
and  for
for ![u \in [0,1+d(x_o,y_o)]](https://s0.wp.com/latex.php?latex=u+%5Cin+%5B0%2C1%2Bd%28x_o%2Cy_o%29%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Since for any
. Since for any  ,
,  ,
, 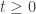
 it is easy to see that
it is easy to see that  , for some constant
, for some constant 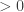 . Hence
. Hence 

The following theorem is known as the Hopf–Rinow theorem, it provides a necessary and sufficient condition for the completeness of the metric space  .
.
Proposition: The metric space  is complete (i.e. Cauchy sequences are convergent) if and only the compact sets are the closed and bounded sets.
is complete (i.e. Cauchy sequences are convergent) if and only the compact sets are the closed and bounded sets.
Proof: It is clear that if closed and bounded sets are compact then the metric space  is complete; It comes from the fact that Cauchy sequence are convergent if and only if they have at least one cluster value. So, we need to prove that closed and bounded sets for the distance
is complete; It comes from the fact that Cauchy sequence are convergent if and only if they have at least one cluster value. So, we need to prove that closed and bounded sets for the distance  are compact provided that
are compact provided that  is complete. To check this, it is enough to prove that closed balls are compact. Let
is complete. To check this, it is enough to prove that closed balls are compact. Let 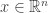 . Observe that if the closed ball
. Observe that if the closed ball  is compact for some
is compact for some  , then
, then  is closed for any
is closed for any  . Define
. Define  Since
Since  induces the usual topology of
induces the usual topology of  ,
,  . Let us assume that
. Let us assume that  and let us show that it leads to a contradiction. We first show that
and let us show that it leads to a contradiction. We first show that  is compact. Since
is compact. Since  is assumed to be complete, it suffices to prove that
is assumed to be complete, it suffices to prove that  is totally bounded: That is, for every
is totally bounded: That is, for every 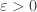 there is a finite set
there is a finite set  such that every point of
such that every point of  belongs to a
belongs to a  -neighborhood of
-neighborhood of  .
.
So, let 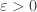 small enough. By definition of
small enough. By definition of 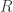 , the ball
, the ball  is compact; It is therefore totally bounded. We can find a finite set
is compact; It is therefore totally bounded. We can find a finite set  such that every point of
such that every point of  lies in a
lies in a  -neighborhood of
-neighborhood of  . Let now
. Let now  . We claim that there exists
. We claim that there exists  such that
such that  . If
. If  , there is nothing to prove, we may therefore assume that
, there is nothing to prove, we may therefore assume that  . Consider then a sub-unit curve
. Consider then a sub-unit curve ![\gamma: [0,R+\varepsilon / 4]](https://s0.wp.com/latex.php?latex=%5Cgamma%3A+%5B0%2CR%2B%5Cvarepsilon+%2F+4%5D&bg=ffffff&fg=333333&s=0&c=20201002) such that
such that  ,
,  . Let
. Let  We have
We have  . On the other hand,
. On the other hand,  As a consequence,
As a consequence,  In every case, there exists therefore
In every case, there exists therefore  such that
such that  . We may then pick
. We may then pick 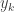 in
in  such that
such that  . From the triangle inequality, we have
. From the triangle inequality, we have  . So, at the end, it turns out that every point of
. So, at the end, it turns out that every point of  lies in a
lies in a  -neighborhood of
-neighborhood of  . This shows that
. This shows that  is totally bounded and therefore compact because
is totally bounded and therefore compact because  is assumed to be complete. Actually, the previous argument shows more, it shows that if every point of
is assumed to be complete. Actually, the previous argument shows more, it shows that if every point of  lies in a
lies in a  -neighborhood of a finite
-neighborhood of a finite  , then every point of
, then every point of  will lie
will lie  -neighborhood of
-neighborhood of  , so that the ball
, so that the ball  is also compact. This contradicts the fact the definition of
is also compact. This contradicts the fact the definition of 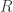 . Therefore every closed ball is a compact set, due to the arbitrariness of
. Therefore every closed ball is a compact set, due to the arbitrariness of 

Checking that the metric space  is complete is not always easy in concrete situations. From the Hopf-Rinow theorem, it suffices to prove that the closed balls are compact. The following proposition is therefore useful.
is complete is not always easy in concrete situations. From the Hopf-Rinow theorem, it suffices to prove that the closed balls are compact. The following proposition is therefore useful.
Proposition: Suppose that the vector fields  ‘s have globally Lipschitz coefficients . Then the closed ball
‘s have globally Lipschitz coefficients . Then the closed ball  is compact for every
is compact for every 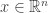 and
and  . As a consequence the metric space
. As a consequence the metric space  is complete.
is complete.
Proof: By the hypothesis on the 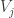 ‘s there exists a constant
‘s there exists a constant  such
such
that  for any
for any 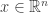 . Fix
. Fix  and let
and let ![\gamma:[0,T]\to\mathbb{R}^n](https://s0.wp.com/latex.php?latex=%5Cgamma%3A%5B0%2CT%5D%5Cto%5Cmathbb%7BR%7D%5En&bg=ffffff&fg=333333&s=0&c=20201002) , be a sub-unit curve such that
, be a sub-unit curve such that  Letting
Letting  we obtain
we obtain  We infer that
We infer that  , for some
, for some  depending only on
depending only on 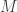 . Integrating the latter inequality one has
. Integrating the latter inequality one has ![\|\gamma(t)\| \leq (A+\| x_o \|) e^{\frac{C}{2}T},\quad t\in [0,T]](https://s0.wp.com/latex.php?latex=%5C%7C%5Cgamma%28t%29%5C%7C+%5Cleq+%28A%2B%5C%7C+x_o+%5C%7C%29+e%5E%7B%5Cfrac%7BC%7D%7B2%7DT%7D%2C%5Cquad+t%5Cin+%5B0%2CT%5D&bg=ffffff&fg=333333&s=0&c=20201002) . for some constant
. for some constant  . The previous estimate shows in particular, that
. The previous estimate shows in particular, that  We conclude that
We conclude that  is Euclidean compact. Since the metric and the Euclidean topology coincide, it is also
is Euclidean compact. Since the metric and the Euclidean topology coincide, it is also  -compact
-compact 
Completeness of the metric space  is related to the essential self-adjointness of the Laplace-Beltrami operator.
is related to the essential self-adjointness of the Laplace-Beltrami operator.
Theorem: If the metric space  is complete, then the Laplace-Beltrami operator
is complete, then the Laplace-Beltrami operator  is essentially self-adjoint.
is essentially self-adjoint.
Proof: We know that if there exists an increasing sequence  such that
such that  on
on  , and
, and  , as
, as 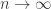 , then the operator
, then the operator  is essentially self-adjoint. We are therefore reduced to prove the existence of such a sequence. Let us fix a base point
is essentially self-adjoint. We are therefore reduced to prove the existence of such a sequence. Let us fix a base point  . We can find an exhaustion function
. We can find an exhaustion function  such that
such that  By the completeness of
By the completeness of  and the Hopf-Rinow theorem, the level sets
and the Hopf-Rinow theorem, the level sets  are relatively compact and, furthermore,
are relatively compact and, furthermore,  as
as  . We now pick an increasing sequence of functions
. We now pick an increasing sequence of functions  such that
such that  on
on ![[0,n]](https://s0.wp.com/latex.php?latex=%5B0%2Cn%5D&bg=ffffff&fg=333333&s=0&c=20201002) ,
,  outside
outside ![[0,2n]](https://s0.wp.com/latex.php?latex=%5B0%2C2n%5D&bg=ffffff&fg=333333&s=0&c=20201002) , and
, and  . If we set
. If we set  , then we have
, then we have  ,
,  on
on  as
as 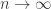 , and
, and 

,
. Show that
is a 2-dimensional smooth manifold homeomorphic to the torus
.
be the stereographic projection from the north pole
, and
be the stereographic projection from the south pole
.
,
.
is a non constant polynomial, the map
,
is smooth.
is smooth, find a condition on
so that
,
is smooth.
is onto.
is dense in
.
