In the previous lectures, we have seen that if L is an essentially self-adjoint diffusion operator with respect to a measure, then by using the spectral theorem one can define a self-adjoint strongly continuous contraction semigroup on L2 with generator L. This semigroup is moreover positivity preserving and a contraction on the space of bounded square integrable functions. Our goal, in this lecture, is to define, for  , the semigroup on
, the semigroup on  . This can be done by using the Riesz–Thorin interpolation theorem that we remind below. In this subsection, in order to simplify the notations we simply denote
. This can be done by using the Riesz–Thorin interpolation theorem that we remind below. In this subsection, in order to simplify the notations we simply denote  by
by  . We first start with general comments about semigroups in Banach spaces.
. We first start with general comments about semigroups in Banach spaces.
Let  be a Banach space (which for us will be
be a Banach space (which for us will be  ,
,  ).
).
We first have the following basic definition.
Definition: A family of bounded operators  on
on  is called a contraction semigroup if:
is called a contraction semigroup if:
 and for
and for  ,
,  ;
;- For each
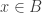 and
and 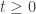 ,
,  .
.
A contraction semigroup  on
on  is moreover said to be strongly continuous if for each
is moreover said to be strongly continuous if for each 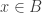 , the map
, the map  is continuous.
is continuous.
In this Lecture, we will prove the following result:
Theorem: let 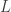 be an essentially self-adjoint diffusion operator. Denote by
be an essentially self-adjoint diffusion operator. Denote by  the self-adjoint strongly continuous semigroup associated to
the self-adjoint strongly continuous semigroup associated to 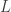 and constructed on
and constructed on  thanks to the spectral theorem. Let
thanks to the spectral theorem. Let  . On
. On  , there exists a unique contraction semigroup
, there exists a unique contraction semigroup  such that for
such that for  ,
,  . The semigroup
. The semigroup  is moreover strongly continuous for
is moreover strongly continuous for  .
.
This theorem can be proved by using two sets of methods: Hille-Yosida theory on one hand and interpolation theory on the other hand. We shall use interpolation theory in  space which takes advantage of the fact that
space which takes advantage of the fact that  only needs to be constructed on
only needs to be constructed on 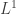 and
and 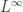 . The Hille-Yosida method starts from the generator and we sketch it below.
. The Hille-Yosida method starts from the generator and we sketch it below.
Definition:
Let  be a strongly continuous contraction semigroup on a Banach space
be a strongly continuous contraction semigroup on a Banach space  . There exists a closed and densely defined operator
. There exists a closed and densely defined operator  where
where  such that for
such that for  ,
,  The operator
The operator  is called the generator of the semigroup
is called the generator of the semigroup  . We also say that
. We also say that  generates
generates  .
.
The following important theorem is due to Hille and Yosida and provides, through spectral properties, a characterization of closed operators that are generators of contraction semigroups.
Let  be a densely defined closed operator. A constant
be a densely defined closed operator. A constant  is said to be in the spectrum of
is said to be in the spectrum of  if the the operator
if the the operator  is not bijective. In that case, it is a consequence of the closed graph theorem that if
is not bijective. In that case, it is a consequence of the closed graph theorem that if 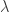 is not in the spectrum of
is not in the spectrum of  , then the operator
, then the operator  has a bounded inverse. The spectrum of an operator
has a bounded inverse. The spectrum of an operator  shall be denoted
shall be denoted  .
.
Theorem: A necessary and sufficient condition that a densely defined closed operator $A$ generates a strongly continuous contraction semigroup is that:
These two conditions are unfortunately difficult to directly check for diffusion operators.
We can bypass the study of the closure in  of a diffusion operator by using interpolation theory.
of a diffusion operator by using interpolation theory.
Theorem: (Riesz-Thorin interpolation theorem) Let  , and
, and  . Define
. Define  by
by  If
If 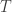 is a linear map such that
is a linear map such that  and
and  then, for every
then, for every  ,
,  Hence
Hence 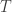 extends uniquely as a bounded map from
extends uniquely as a bounded map from  to
to  with
with 
The statement that 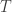 is a linear map such that
is a linear map such that  and
and  means that there exists a map
means that there exists a map  with
with  and
and  In such a case,
In such a case, 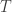 can be uniquely extended to bounded linear maps
can be uniquely extended to bounded linear maps  ,
,  . With a slight abuse of notation, these two maps are both denoted by
. With a slight abuse of notation, these two maps are both denoted by 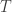 in the theorem.
in the theorem.
The proof of the theorem can be found in this post by Tao.
One of the (numerous) beautiful applications of the Riesz-Thorin theorem is to construct diffusion semigroups on  by interpolation. More precisely, let
by interpolation. More precisely, let 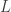 be an essentially self-adjoint diffusion operator. We denote by
be an essentially self-adjoint diffusion operator. We denote by  the self-adjoint strongly continuous semigroup associated to
the self-adjoint strongly continuous semigroup associated to 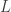 constructed on
constructed on  thanks to the spectral theorem. We recall that
thanks to the spectral theorem. We recall that  satisfies the submarkov property: That is, if
satisfies the submarkov property: That is, if  is a function in
is a function in  , then
, then  .
.
Theorem: The space  is invariant under
is invariant under  and
and  may be extended from
may be extended from  to a contraction semigroup
to a contraction semigroup  on
on  for all
for all  : For
: For  ,
,  These semigroups are consistent in the sense that for
These semigroups are consistent in the sense that for  ,
, 
Proof: If  which is a subset of
which is a subset of  , then
, then  This implies
This implies  The conclusion follows then from the Riesz-Thorin interpolation theorem
The conclusion follows then from the Riesz-Thorin interpolation theorem 
Exercise: Show that if  and
and  with
with  then,
then, 
Exercise:
- Show that for each
 , the
, the  -valued map
-valued map  is continuous.
is continuous.
- Show that for each
 ,
,  , the
, the  -valued map
-valued map  is continuous.
is continuous.
- Finally, by using the reflexivity of
 , show that for each
, show that for each  and every
and every 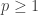 , the
, the  -valued map
-valued map  is continuous.
is continuous.
We mention, that in general, the  valued map
valued map  is not continuous.
is not continuous.
Due to the consistency property, we always remove the subscript  from
from  and only use the notation
and only use the notation  .
.
To finish this Lecture, we finally connect the heat semigroup in  to
to  solutions of the heat equation.
solutions of the heat equation.
Proposition: Let  ,
,  , and let
, and let  Then, if
Then, if 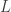 is elliptic with smooth coefficients,
is elliptic with smooth coefficients,  is smooth on
is smooth on  and is a strong solution of the Cauchy problem
and is a strong solution of the Cauchy problem 
Proof: The proof is identical to the 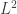 case. For
case. For  , we have
, we have




Therefore  is a weak solution of the equation
is a weak solution of the equation  . Since
. Since  is smooth it is also a strong solution
is smooth it is also a strong solution  .
.
We now address the uniqueness of solutions. As in the 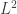 case, we assume that
case, we assume that 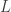 is elliptic with smooth coefficients and that there is a sequence
is elliptic with smooth coefficients and that there is a sequence  ,
,  , such that
, such that  on
on 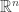 , and
, and  , as
, as 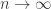 .
.
Proposition: Let  be a non negative function such that
be a non negative function such that  and such that for every
and such that for every 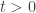 ,
,  , where
, where  . Then
. Then  .
.
Proof: Let  and
and  . Since
. Since  is a subsolution with the zero initial data, for any
is a subsolution with the zero initial data, for any  ,
,




On the other hand, integrating by parts yields

Observing that

we obtain the following estimate.



Combining with the previous conclusion we obtain ,

By using the previous inequality with an increasing sequence  ,
,  , such that
, such that  on
on 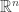 , and
, and  , as
, as 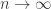 , and letting
, and letting 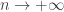 , we obtain
, we obtain
 thus
thus 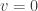
 .
.
As a consequence of this result, any solution in  ,
,  of the heat equation
of the heat equation  is uniquely determined by its initial condition, and is therefore of the form
is uniquely determined by its initial condition, and is therefore of the form  . We stress that without further conditions, this result fails when
. We stress that without further conditions, this result fails when 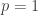 or
or  .
.
be a locally subelliptic and essentially self-adjoint diffusion operator. Let
be the semigroup generated by
. By using the maximum principle for parabolic pdes, prove that if
is in
, then
.
be an essentially self-adjoint diffusion operator. Denote by
the semigroup generated by
in
.
, the
-valued map
is continuous.
,
, the
-valued map
is continuous.
, show that for each
and every
, the
-valued map
is continuous.
