Let  be a smooth, connected manifold with dimension
be a smooth, connected manifold with dimension 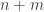 . We assume that
. We assume that  is equipped with a Riemannian foliation
is equipped with a Riemannian foliation  with bundle like metric
with bundle like metric  and totally geodesic
and totally geodesic  -dimensional leaves.
-dimensional leaves.
We define the canonical variation of  as the one-parameter family of Riemannian metrics:
as the one-parameter family of Riemannian metrics:

We now introduce some tensors and definitions that will play an important role in the sequel.
For  , there is a unique skew-symmetric endomorphism
, there is a unique skew-symmetric endomorphism  such that for all horizontal vector fields
such that for all horizontal vector fields  and
and  ,
,

where  is the torsion tensor of
is the torsion tensor of  . We then extend
. We then extend  to be 0 on
to be 0 on  . If
. If  is a local vertical frame, the operator
is a local vertical frame, the operator  does not depend on the choice of the frame and shall concisely be denoted by
does not depend on the choice of the frame and shall concisely be denoted by  . For instance, if
. For instance, if  is a K-contact manifold equipped with the Reeb foliation, then
is a K-contact manifold equipped with the Reeb foliation, then 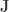 is an almost complex structure,
is an almost complex structure,  .
.
The horizontal divergence of the torsion  is the
is the  tensor which is defined in a local horizontal frame
tensor which is defined in a local horizontal frame  by
by

The  -adjoint of
-adjoint of  will be denoted
will be denoted  .
.
In the sequel, we shall need to perform computations on one-forms. For that purpose we introduce some definitions and notations on the cotangent bundle.
We say that a one-form to be horizontal (resp. vertical) if it vanishes on the vertical bundle 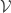 (resp. on the horizontal bundle
(resp. on the horizontal bundle  ). We thus have a splitting of the cotangent space
). We thus have a splitting of the cotangent space

The metric  induces then a metric on the cotangent bundle which we still denote
induces then a metric on the cotangent bundle which we still denote  . By using similar notations and conventions as before we have for every
. By using similar notations and conventions as before we have for every  in
in  ,
,

By using the duality given by the metric  ,
,  tensors can also be seen as linear maps on the cotangent bundle
tensors can also be seen as linear maps on the cotangent bundle  . More precisely, if
. More precisely, if  is a
is a  tensor, we will still denote by
tensor, we will still denote by  the fiberwise linear map on the cotangent bundle which is defined as the
the fiberwise linear map on the cotangent bundle which is defined as the  -adjoint of the dual map of
-adjoint of the dual map of  . The same convention will be made for any
. The same convention will be made for any 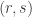 tensor.
tensor.
We define then the horizontal Ricci curvature  as the fiberwise symmetric linear map on one-forms such that for every smooth functions
as the fiberwise symmetric linear map on one-forms such that for every smooth functions 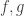 ,
,

where  is the Ricci curvature of the connection
is the Ricci curvature of the connection  .
.
If  is a horizontal vector field and
is a horizontal vector field and 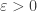 , we consider the fiberwise linear map from the space of one-forms into itself which is given for
, we consider the fiberwise linear map from the space of one-forms into itself which is given for  and
and  by
by

We observe that  is skew-symmetric for the metric
is skew-symmetric for the metric  so that
so that  is a
is a  -metric connection.
-metric connection.
If  is a one-form, we define the horizontal gradient of
is a one-form, we define the horizontal gradient of  in a local frame as the
in a local frame as the  tensor
tensor

Similarly, we will use the notation

Finally, we will still denote by  the covariant extension on one-forms of the horizontal Laplacian. In a local horizontal frame, we have thus
the covariant extension on one-forms of the horizontal Laplacian. In a local horizontal frame, we have thus

For 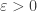 , we consider the following operator which is defined on one-forms by
, we consider the following operator which is defined on one-forms by

where the adjoint is understood with respect to the metric  . It is easily seen that, in a local horizontal frame,
. It is easily seen that, in a local horizontal frame,

We can also consider the operator which is defined on one-forms by

It is clear that for every smooth one-form  on
on  and every
and every  the following holds
the following holds

The following theorem that was proved in this paper is the main result of the lecture:
Theorem: Let  . For every
. For every  , we have
, we have

Proof:
We only sketch the proof and refer to the original paper for the details. If  is a local vertical frame of the leaves, we denote
is a local vertical frame of the leaves, we denote

where  is the the projection of
is the the projection of  onto the vertical cotangent bundle. It does not depend on the choice of the frame and therefore defines a globally defined tensor.
onto the vertical cotangent bundle. It does not depend on the choice of the frame and therefore defines a globally defined tensor.
Also, let us consider the map  which is given in a local coframe
which is given in a local coframe  ,
, 

A direct computation shows then that


Thus, we just need to prove that if  is the operator defined on one-forms by
is the operator defined on one-forms by

then for any  ,
,

A computation in local frame shows that

which completes the proof 
We also have the following Bochner’s type identity.
Theorem: For any  ,
,

We now turn to probabilistic applications.
We denote by  the horizontal Brownian motion on
the horizontal Brownian motion on  . The lifetime of the process is denoted by
. The lifetime of the process is denoted by  . We assume that the metric
. We assume that the metric  is complete and
is complete and  is bracket generating. As a consequence, one can define
is bracket generating. As a consequence, one can define  the heat semigroup associated to
the heat semigroup associated to  as being the semigroup generated by the self-adjoint extension of
as being the semigroup generated by the self-adjoint extension of  .
.
We define a process  by the formula
by the formula

where the process  is the stochastic parallel transport with respect to the connection
is the stochastic parallel transport with respect to the connection  along the paths of
along the paths of  . The multiplicative functional
. The multiplicative functional  is defined as the solution of the following ordinary differential equation
is defined as the solution of the following ordinary differential equation

Observe that the process  is a solution of the following covariant Stratonovitch stochastic differential equation:
is a solution of the following covariant Stratonovitch stochastic differential equation:
![d[\tau^\varepsilon_t \alpha(X_t)]=\tau^\varepsilon_t\left( \nabla_{\circ dX_t}-\mathfrak{T}_{\circ dX_t}^{\varepsilon}-\frac{1}{2} \left( \frac{1}{ \varepsilon}\mathbf{J}^2-\frac{1}{\varepsilon} \delta_\mathcal{H} T+ \mathfrak{Ric}_{\mathcal{H}}\right)dt\right) \alpha(X_t),~~\tau_0=\mathbf{Id},](https://s0.wp.com/latex.php?latex=d%5B%5Ctau%5E%5Cvarepsilon_t+%5Calpha%28X_t%29%5D%3D%5Ctau%5E%5Cvarepsilon_t%5Cleft%28+%5Cnabla_%7B%5Ccirc+dX_t%7D-%5Cmathfrak%7BT%7D_%7B%5Ccirc+dX_t%7D%5E%7B%5Cvarepsilon%7D-%5Cfrac%7B1%7D%7B2%7D+%5Cleft%28+%5Cfrac%7B1%7D%7B+%5Cvarepsilon%7D%5Cmathbf%7BJ%7D%5E2-%5Cfrac%7B1%7D%7B%5Cvarepsilon%7D+%5Cdelta_%5Cmathcal%7BH%7D+T%2B+%5Cmathfrak%7BRic%7D_%7B%5Cmathcal%7BH%7D%7D%5Cright%29dt%5Cright%29+%5Calpha%28X_t%29%2C%7E%7E%5Ctau_0%3D%5Cmathbf%7BId%7D%2C&bg=ffffff&fg=333333&s=0&c=20201002)
where  is any smooth one-form.
is any smooth one-form.
From Gronwall’s lemma and the fact that  is an isometry, we easily deduce that
is an isometry, we easily deduce that
Lemma: Let 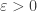 . Assume that there exists a constant
. Assume that there exists a constant  such that for every
such that for every  ,
,

Then, there exists a constant  , such that for every
, such that for every 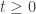 ,
,

For  , as usual we will denote
, as usual we will denote

Theorem: Assume that there exists a constant  such that for every
such that for every  ,
,

Let  be a one-form on
be a one-form on  which is smooth and compactly supported. The unique solution in
which is smooth and compactly supported. The unique solution in 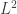 of the Cauchy problem:
of the Cauchy problem:

is given by

Proof:
This is Feynman-Kac formula.
Sketch of the proof.
It is proved in this course, that the operator

is essentially self-adjoint on the space of smooth and compactly supported one-forms. Thus, from the assumption,  is the generator of a bounded semigroup
is the generator of a bounded semigroup  in
in 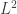 that uniquely solves the above Cauchy problem.
that uniquely solves the above Cauchy problem.
From the Bochner’s identity, one has
 .
.
From Shigekawa (L^p contraction for vector valued semigroups), this implies the a priori pointwise bound
 .
.
We now claim that the process
 ,
,
is a local martingale. Indeed, from Ito’s formula and the definition of  , we have
, we have


We now conclude from the fact that the bounded variation part of

is given by  .
.
Form the previous estimates, we conclude that  is a martingale
is a martingale 
Corollary: Let 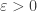 . Assume that there exists a constant
. Assume that there exists a constant  such that for every
such that for every  ,
,

Then, for  , and
, and 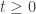

As a consequence,  .
.
Proof: Let  .
.
We have

Thus, from the previous theorem

This representation implies the bound

It is well-known that this type of gradient bound implies the stochastic completeness of  . More precisely, we can adapt an argument of Bakry. Let
. More precisely, we can adapt an argument of Bakry. Let  , we have
, we have



By means of Cauchy-Schwarz inequality we
find

We now apply the previous inequality with  , where
, where  is an increasing sequence in
is an increasing sequence in  ,
,  , such that
, such that  on
on  , and
, and  , as
, as 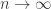 .
.
By monotone convergence theorem we have  for every
for every  . We conclude that the
. We conclude that the
left-hand side converges to  . Since the right-hand side converges to zero, we reach the conclusion
. Since the right-hand side converges to zero, we reach the conclusion

Since it is true for every  , it follows that
, it follows that  .
.

be a linear operator such that:
is a local operator, that is if
on a neighborhood of
then
;
has a global maximum at
with
then
.
and
,
,
and
are continuous functions on
such that for every
,
and the matrix
is symmetric and nonnegative.
are
functions and
are also
then,
is a
function and
is also
,
, let us consider the diffusion operator
where
is a
function. Show that
is symmetric with respect to the measure
.
, let us consider the operator
where
is the divergence operator defined on a
function
by
is a
field of non negative and symmetric matrices. Show that
is a diffusion operator which is symmetric with respect to the Lebesgue measure.
, we consider the divergence form operator
is a smooth field of positive and symmetric matrices that satisfies
. Show that with respect to the Lebesgue measure, the operator
is essentially self-adjoint on
