Lecture 1. The Paul Levy’s stochastic area formula

Posted on June 30, 2016 by Fabrice Baudoin

When studying functionals of a Brownian motion, it may be useful to embed this functional into a larger dimensional Markov process.

Consider the case of the Levy area
S_t=\int_0^t B^1_s dB^2_s-B^2_s dB^1_s,
where B_t=(B^1_t,B^2_t), t \ge 0, is a two dimensional Brownian motion started at 0. We can write
S_t=\int_{B[0,t]} \alpha
where \alpha=xdy-ydx. Since d\alpha =2 dx \wedge dy, we interpret S_t as (two times) the algebraic area swept out in the plane by the Brownian curve up to time t. The process (S_t)_{t \ge 0} is not a Markov process in its own natural filtration. However, if we consider the 3-dimensional process
X_t=(B^1_t,B^2_t,S_t),
then X_t is solution of a stochastic differential equation
dX^1_t =dB^1_t

dX^2_t =dB^2_t

dX^3_t =-X^2_t dB^1_t+X^1_t dB^2_t

As a consequence X_t is a Markov process with generator

L=\frac{1}{2} (X^2+Y^2)
where X,Y are the following vector fields
X=\frac{\partial}{\partial x}-y \frac{\partial}{\partial z}
Y=\frac{\partial}{\partial y}+x \frac{\partial}{\partial z}.
Observe that the Lie bracket

[X,Y]=XY-YX =2 \frac{\partial}{\partial z}.
Thus, for every x \in \mathbb{R}^3, (X(x),Y(x), [X,Y](x)) is a basis of \mathbb{R}^3. From the celebrated Hormander’s theorem, this implies that for every t > 0 the random variable X_t has a smooth density with respect to the Lebesgue measure of \mathbb{R}^3. In particular S_t also has smooth density whenever t>0. We are interested in an expression for this density. The first idea is to reduce the complexity of the random variable X_t by making use of symmetries.

Lemma: Let r_t=\| B_t \|=\sqrt{ (B^1_t)^2 +(B^2_t)^2 }, t \ge 0. Then, the couple

(r_t , S_t)_{t \ge 0}
is a Markov process with generator

\mathcal{L}=\frac{1}{2r} \frac{\partial}{\partial r}+\frac{1}{2} \frac{\partial^2}{\partial r^2}+\frac{1}{2}r^2 \frac{\partial^2}{\partial s^2}

Proof:
From Ito’s formula, we have

dr_t =\frac{dt}{2 r_t}+\frac{B^1_t dB^1_t+B^2_t dB^2_t}{ \sqrt{ (B^1_t)^2 +(B^2_t)^2 }}

dS_t=r_t \frac{B^1_t dB^2_t-B^2_t dB^1_t}{ \sqrt{ (B^1_t)^2 +(B^2_t)^2 }}.

Since the two processes

\beta_t=\int_0^t \frac{B^1_s dB^1_s+B^2_s dB^2_s}{ \sqrt{ (B^1_s)^2 +(B^2_s)^2 }} 

\gamma_t=\int_0^t \frac{B^1_s dB^2_s-B^2_s dB^1_s}{ \sqrt{ (B^1_s)^2 +(B^2_s)^2 }},

are two independent Brownian motions, the conclusion easily follows. \square

We are now ready to prove the celebrated Levy’s area formula.

Theorem: For t>0 and x \in \mathbb{R}^2, and \lambda >0

\mathbb{E}\left( e^{i\lambda S_t} | B_t=x\right)=\frac{\lambda t}{\sinh \lambda t} e^{-\frac{\|x\|^2}{2t}(\lambda t \coth \lambda t -1) }.

Proof:
First, we observe that by rotational symmetry of the Brownian motion (B_t)_{t \ge 0}, we have

\mathbb{E}\left( e^{i\lambda S_t} | B_t=x\right)=\mathbb{E}\left( e^{i\lambda S_t} | \| B_t \| =\| x \| \right).
Then, according to the previous lemma,

\mathbb{E}\left( e^{i\lambda S_t} | \| B_t \| =\| x \| \right)=\mathbb{E}\left( e^{i\lambda \gamma_{\int_0^t r_s^2 ds}} | r_t =\| x \| \right),
where \gamma_t is a Brownian motion independent from r. We deduce

\mathbb{E}\left( e^{i\lambda S_t} | B_t=x\right)=\mathbb{E}\left( e^{-\frac{\lambda^2}{2} \int_0^t r_s^2 ds} | r_t =\| x \| \right),
As we have seen, r_t solves a stochastic differential equation

dr_t =\frac{dt}{2 r_t}+d\beta_t,
where \beta is a one-dimensional Brownian motion.
One considers then the new probability

\mathbb{P}_{/ \mathcal{F}_t}^\lambda = \exp \left(- \lambda \int_0^t r_s d\beta_s -\frac{\lambda^2}{2} \int_0^t r_s^2 ds \right)\mathbb{P}_{/ \mathcal{F}_t},
where \mathcal{F} is the natural filtration of \beta. Observe that

\int_0^t r_s d\beta_s =\int_0^t r_s dr_s -\frac{t}{2} =\frac{1}{2} r_t^2 -t

Therefore

\exp \left( -\lambda \int_0^t r_s d\beta_s -\frac{\lambda^2}{2} \int_0^t r_s^2 ds \right)=e^{\lambda t} \exp \left( -\frac{\lambda}{2} r_t^2 -\frac{\lambda^2}{2} \int_0^t r_s^2 ds \right)

In particular, one deduces that

\exp \left( -\lambda \int_0^t r_s d\beta_s -\frac{\lambda^2}{2} \int_0^t r_s^2 ds \right) \le e^{\lambda t},
which proves that \exp \left( -\lambda \int_0^t r_s d\beta_s -\frac{\lambda^2}{2} \int_0^t r_s^2 ds \right) is a martingale. By using this change of probability, if f is a bounded and Borel function, we have

\mathbb{E}\left( f(r_t) e^{-\frac{\lambda^2}{2} \int_0^t r_s^2 ds} \right) =e^{-\lambda t} \mathbb{E}^\lambda \left(f(r_t) \exp \left( \frac{\lambda}{2} r_t^2 +\frac{\lambda^2}{2} \int_0^t r_s^2 ds \right) e^{-\frac{\lambda^2}{2} \int_0^t r_s^2 ds} \right) =e^{-\lambda t} \mathbb{E}^\lambda \left(f(r_t) \exp \left( \frac{\lambda}{2} r_t^2 \right) \right).
Putting things together, we are thus let with the computation of the distribution of r_t under the probability \mathbb{P}^\lambda. From Girsanov’s theorem, the process

\beta^\lambda_t=\beta_t +\lambda \int_0^t r_s ds

is a Brownian motion under the probability \mathbb{P}^\lambda. Thus

dr_t =\left( \frac{1}{2 r_t} -\lambda r_t \right) dt+d\beta^\lambda_t.

In law, this is the stochastic differential equation solved by \| Y_t \| where

dY_t =-\lambda Y_t dt +dB^\lambda_t, \quad Y_0=0.

We deduce that r_t is distributed as \| Y_t \|, the norm of a two-dimensional Ornstein Uhlenbeck process with parameter -\lambda. Since Y_t is a Gaussian random variable with mean 0 and variance \frac{1-e^{-2\lambda t}}{2\lambda} \mathbf{Id}, the conclusion follows from standard computations about the Gaussian distribution. \square

This formula is due to Paul Levy who originally used a series expansion of the Brownian motion. The proof we present here is due to Marc Yor.

The Levy’s area formula has several interesting consequences. First, when x=0, we deduce that

\mathbb{E}\left( e^{i\lambda S_t} | B_t=0\right)=\frac{\lambda t}{\sinh \lambda t}.

This gives a formula for the characteristic function of the algebraic stochastic area within the Brownian loop with length t. Inverting this Fourier transform yields

\mathbb{P} \left( S_t \in ds | B_t=0 \right)=\frac{\pi}{2t} \frac{1}{\cosh^2 \left( \frac{\pi s}{t}\right)} ds.

Next, integrating the Levy’s area formula with respect to the distribution of B_t yields the characteristic function of S_t:

\mathbb{E}\left( e^{i\lambda S_t} \right)=\frac{1}{\cosh (\lambda t)}

Inverting this Fourier transform yields

\mathbb{P} \left( S_t \in ds \right)=\frac{\pi}{t} \frac{1}{\cosh \left( \frac{\pi s}{2t}\right)} ds.

One may deduce from it the following formula (due to Biane-Yor): For \alpha>0,

\mathbb{E} (|S_t|^\alpha)=\frac{2^{\alpha+2} \Gamma(1+\alpha)}{\pi^{1+\alpha}} L(1+\alpha) t^\alpha,

where L(s)=\sum_{n=0}^{+\infty} \frac{(-1)^n}{(2n+1)^s} is the Dirichlet function. This provides an unexpected and fascinating connection with the Riemann zeta function.

Posted in Diffusions on foliated manifolds | 2 Comments

Summer school in probability

Posted on June 30, 2016 by Fabrice Baudoin
Northwestern Summer School in Probability, 11-21 July 2016
 
 

Website of the summer school

I will be lecturing in Northwestern University from July 11 to July 21. Lectures will be posted on the blog.  The main topic will be the study of diffusion processes on foliated spaces.
Posted in Diffusions on foliated manifolds | Leave a comment

Lecture 6. Hypocoercivity

Posted on November 2, 2014 by Fabrice Baudoin

Hypocoercivity is a concept introduced by C. Villani. It aims to give quantitative estimates for the convergence to equilibrium of hypoelliptic models. In this last lecture, I present an approach to hypocoercivity which parallels the Bakry-Emery approach to hypercontractivity. It is only based on local computations and provides quite explicit convergence rates.

The lecture is based on section 7 of the Lecture Notes.

Posted in Hypoelliptic operators | Leave a comment

Lecture 5. The horizontal Bonnet-Myers

Posted on November 2, 2014 by Fabrice Baudoin

This lecture gives the proof of the horizontal Bonnet-Myers theorem for Riemannian foliations with totally geodesic leaves. The proof relies on diffusion semigroups methods.

Part 1 covers sections 6.1 and half of section 6.2 in the Lecture Notes and part 2 cover the other half of section 6.2.

Posted in Hypoelliptic operators | Leave a comment

Lecture 4. The generalized curvature dimension inequality

Posted on November 2, 2014 by Fabrice Baudoin

In this Lecture 4, we use the Weitzenbock formula proved in the previous lecture to prove a generalized curvature dimension inequality, from which we will deduce Li-Yau type estimates for the horizontal heat kernel.

Part 1 covers sections 4.3, 4.4 and 5.1 in the Lecture Notes and Part 2 covers sections 5.2, 5.3 and 5.4.

Posted in Hypoelliptic operators | Leave a comment

Lecture 3. Hopf fibration. Transverse Weitzenbock formulas

Posted on October 11, 2014 by Fabrice Baudoin

In this lecture we continue the study of the Hopf fibration and compute the horizontal heat kernel of this fibration. In the second part of the lecture, we come back to the general framework of Riemannian foliations and introduce a canonical sub-Laplacian on one-form for which we prove Bochner-Weitzenbock type identities.

As we have seen in the previous lecture, the radial part of the Laplacian of the Hopf fibration is given

\overline{\Delta}_{\mathcal{H}}=\frac{\partial^2}{\partial r^2}+((2n-1)\cot r-\tan r)\frac{\partial}{\partial r}+\tan^2r\frac{\partial^2}{\partial \theta^2}

We can observe that \overline{\Delta}_{\mathcal{H}} is symmetric with respect to the measure

d\overline{\mu}=\frac{2\pi^n}{\Gamma(n)}(\sin r)^{2n-1}\cos r drd\theta,

where the normalization is chosen in such a way that

\int_{-\pi}^{\pi}\int_0^{\frac{\pi}{2}}d\overline{\mu}=\mu(\mathbb S^{2n+1})=\frac{2\pi^{n+1}}{\Gamma (n+1)}.

As mentioned above, the heat kernel at the north pole of \Delta_{\mathcal{H}} only depends on (r, \theta), that is p\left(w e^{i\theta}\cos r ,e^{i\theta}\cos r \right)=\overline{p}_t(r, \theta), where \overline{p}_t is the heat kernel at 0 of \overline{\Delta}_{\mathcal{H}}.

Proposition: For t>0, r\in[0,\frac{\pi}{2}), \theta\in[-\pi,\pi]:

\overline{p}_t(r, \theta)=\frac{\Gamma(n)}{2\pi^{n+1}}\sum_{k=-\infty}^{+\infty}\sum_{m=0}^{+\infty} (2m+|k|+n){m+|k|+n-1\choose n-1}e^{-\lambda_{m,k}t+ik \theta}(\cos r)^{|k|}P_m^{n-1,|k|}(\cos 2r),

where \lambda_{m,k}=4m(m+|k|+n)+2|k|n and

P_m^{n-1,|k|}(x)=\frac{(-1)^m}{2^m m!(1-x)^{n-1}(1+x)^{|k|}}\frac{d^m}{dx^m}((1-x)^{n-1+m}(1+x)^{|k|+m})

is a Jacobi polynomial.

Proof: Similarly to the Heisenberg group case, we observe that \overline{\Delta}_{\mathcal{H}} commutes with \frac{\partial}{\partial \theta}, so the idea is to expand p_t(r, \theta) as a Fourier series in \theta. We can write

\overline{p}_t(r, \theta)=\frac{1}{2\pi} \sum_{k=-\infty}^{+\infty} e^{ik\theta}\phi_k(t,r),

where \phi_k is the fundamental solution at 0 of the parabolic equation

\frac{\partial\phi_k}{\partial t}=\frac{\partial^2\phi_k}{\partial r^2}+((2n-1)\cot r-\tan r)\frac{\partial\phi_k}{\partial r}-k^2\tan^2 r\phi_k.

By writing \phi_k(t,r) in the form

\phi_k(t,r)=e^{-2n|k|t}(\cos r)^{|k|}g_k(t, \cos 2r),

we get

\frac{\partial g_k}{\partial t}=4\mathcal{L}_k(g_k),

where

\mathcal{L}_k=(1-x^2)\frac{\partial^2}{\partial x^2}+[(|k|+1-n)-(|k|+1+n)x]\frac{\partial}{\partial x}.

The eigenvectors of \mathcal{L}_k solve the Jacobi differential equation, and are thus given by the Jacobi polynomials

P_m^{n-1,|k|}(x)=\frac{(-1)^m}{2^m m!(1-x)^{n-1}(1+x)^{|k|}}\frac{d^m}{dx^m}((1-x)^{n-1+m}(1+x)^{|k|+m}),

which satisfy

\mathcal{L}_k(P_m^{n-1,|k|})(x)=-m(m+n+|k|)P_m^{n-1,|k|}(x).

By using the fact that the family (P_m^{n-1,|k|}(x)(1+x)^{|k|/2})_{m\geq0} is an orthogonal basis of L^2([-1,1],(1-x)^{n-1}dx), such that

\int_{-1}^1 P_m^{n-1,|k|}(x)P_l^{n-1,|k|}(x)(1-x)^{n-1}(1+x)^{|k|}dx=\frac{2^{n+|k|}}{2m+|k|+n}\frac{\Gamma(m+n)\Gamma(m+|k|+1)}{\Gamma(m+1)\Gamma(m+n+|k|)}\delta_{ml},

we easily compute the fundamental solution of the operator \frac{\partial }{\partial t}- 4\mathcal{L}_k \square

Note that as a by-product of the previous result we obtain that the L^2 spectrum of -\Delta_\mathcal{H} is given by

\mathbf{Sp} (-\Delta_\mathcal{H}) =\left\{ 4m(m+k+n)+2kn, k \in \mathbb{N}, m \in \mathbb{N} \right\}.

We can give another representation of the heat kernel \overline{p}_t(r,\theta) which is easier to handle analytically. The key idea is to observe that since \Delta and \frac{\partial}{\partial \theta} commute, we formally have

e^{t\Delta_{\mathcal{H}}}=e^{-t\frac{\partial^2}{\partial\theta^2}}e^{t\Delta}.

This gives a way to express the horizontal heat kernel in terms of the Riemannian one.
Let us recall that the Riemannian heat kernel on the sphere \mathbb{S}^{2n+1} is given by

q_t(\cos\delta)=\frac{\Gamma(n)}{2\pi^{n+1}}\sum_{m=0}^{+\infty}(m+n)e^{-m(m+2n)t}C_m^n(\cos \delta),

where, \delta is the Riemannian distance based at the north pole and

C_m^n(x)=\frac{(-1)^m}{2^m}\frac{\Gamma(m+2n)\Gamma(n+1/2)}{\Gamma(2n)\Gamma(m+1)\Gamma(n+m+1/2)}\frac{1}{(1-x^2)^{n-1/2}}\frac{d^m}{dx^m}(1-x^2)^{n+m-1/2},

is a Gegenbauer polynomial. Another expression of q_t (\cos \delta) is

q_t (\cos \delta)= e^{n^2t} \left( -\frac{1}{2\pi \sin \delta} \frac{\partial}{\partial \delta} \right)^n V

where V(t,\delta)=\frac{1}{\sqrt{4\pi t}} \sum_{k \in \mathbb{Z}} e^{-\frac{(\delta-2k\pi)^2}{4t} } is a theta function.

Using the commutation and the formula \cos \delta =\cos r \cos \theta, we then infer the following proposition which is easy to prove

Proposition: For t>0, r\in[0,\pi/2), \theta\in[-\pi,\pi],

\overline{p}_t(r, \theta)=\frac{1}{\sqrt{4\pi t}}\int_{-\infty}^{+\infty}e^{-\frac{(y+i \theta)^2}{4t} }q_t(\cos r\cosh y)dy.

Applications of this formula are given in my paper with Jing Wang. We can, in particular, deduce from it small asymptotics of the kernel when t \to 0. Interestingly, these small-time asymptotics allow to compute explicitly the sub-Riemannian distance.

We now come back to the general framework of a Riemannian foliation.

Let \mathbb{M} be a smooth, connected manifold with dimension n+m. We assume that \mathbb{M} is equipped with a Riemannian foliation \mathcal{F} with bundle like metric g and totally geodesic m-dimensional leaves.

As usual, the sub-bundle \mathcal{V} formed by vectors tangent to the leaves will be referred to as the set of vertical directions and the sub-bundle \mathcal{H} which is normal to \mathcal{V} will be referred to as the set of horizontal directions. The metric g can be split as

g=g_\mathcal{H} \oplus g_{\mathcal{V}},

We define the canonical variation of g as the one-parameter family of Riemannian metrics:

g_{\varepsilon}=g_\mathcal{H} \oplus \frac{1}{\varepsilon }g_{\mathcal{V}}, \quad \varepsilon > 0.

On the Riemannian manifold (\mathbb M,g) there is the Levi-Civita connection that we denote by D, but this connection is not adapted to the study of follations because the horizontal and the vertical bundle may not be parallel. More adapted to the geometry of the foliation is the Bott connection that we now define. In terms of the Levi-Civita connection, the Bott connection writes

\nabla_X Y = \begin{cases} ( D_X Y)_{\mathcal{H}} , \quad X,Y \in \Gamma^\infty(\mathcal{H}) \\ [X,Y]_{\mathcal{H}}, \quad X \in \Gamma^\infty(\mathcal{V}), Y \in \Gamma^\infty(\mathcal{H}) \\ [X,Y]_{\mathcal{V}}, \quad X \in \Gamma^\infty(\mathcal{H}), Y \in \Gamma^\infty(\mathcal{V}) \\ ( D_X Y)_{\mathcal{V}}, \quad X,Y \in \Gamma^\infty(\mathcal{V}) \end{cases}

where the subscript \mathcal H (resp. \mathcal{V}) denotes the projection on \mathcal{H} (resp. \mathcal{V}). Observe that for horizontal vector fields X,Y the torsion T(X,Y) is given by

T(X,Y)=-[X,Y]_\mathcal V.

Also observe that for X,Y \in \Gamma^\infty(\mathcal{V}) we actually have ( D_X Y)_{\mathcal{V}}= D_X Y because the leaves are assumed to be totally geodesic. Finally, it is easy to check that for every \varepsilon > 0, the Bott connection satisfies \nabla g_\varepsilon=0.

Example: Let (\mathbb M, \theta,g) be a K-contact Riemannian manifold. The Bott connection coincides with the Tanno’s connection, which is the unique connection that satisfies:

  • \nabla\theta=0;
  • \nabla T=0;
  • \nabla g=0;
  • T(X,Y)=d\theta(X,Y)T for any X,Y\in \Gamma^\infty(\mathcal{H});
  • {T}(T,X)=0 for any vector field X\in \Gamma^\infty(\mathcal{H}).

    • We now introduce some tensors and definitions that will play an important role in the sequel.

    For Z \in \Gamma^\infty(T\mathbb M), there is a unique skew-symmetric endomorphism J_Z:\mathcal{H}_x \to \mathcal{H}_x such that for all horizontal vector fields X and Y,

    g_\mathcal{H} (J_Z (X),Y)= g_\mathcal{V} (Z,T(X,Y)).

    where T is the torsion tensor of \nabla. We then extend J_{Z} to be 0 on \mathcal{V}_x. If Z_1,\cdots,Z_m is a local vertical frame, the operator \sum_{l=1}^m J_{Z_l}J_{Z_l} does not depend on the choice of the frame and shall concisely be denoted by \mathbf{J}^2. For instance, if \mathbb M is a K-contact manifold equipped with the Reeb foliation, then \mathbf{J} is an almost complex structure, \mathbf{J}^2=-\mathbf{Id}_{\mathcal{H}}.

    The horizontal divergence of the torsion T is the (1,1) tensor which is defined in a local horizontal frame X_1,\cdots,X_n by

    \delta_\mathcal{H} T (X)= \sum_{j=1}^n(\nabla_{X_j} T) (X_j,X), \quad X \in \Gamma^\infty(\mathbb M).

    The g-adjoint of \delta_\mathcal{H}T will be denoted \delta_\mathcal{H} T^*.

    Definition: We say that the Riemannian foliation is of Yang-Mills type if \delta_\mathcal{H} T=0.

    Example: Let (\mathbb M, \theta,g) be a K-contact Riemannian manifold. It is easy to see that the Reeb foliation is of Yang-Mills type if and only if \delta_\mathcal{H} d \theta=0. Equivalently this condition writes \delta_\mathcal{H} J =0. If \mathbb M is a strongly pseudo convex CR manifold with pseudo-Hermitian form \theta, then the Tanno’s connection is the Tanaka-Webster connection. In that case, we have then \nabla J=0 and thus \delta_\mathcal{H} J =0. CR manifold of K-contact type are called Sasakian manifolds. Thus the Reeb foliation on any Sasakian manifold is of Yang-Mills type.

    In the sequel, we shall need to perform computations on one-forms. For that purpose we introduce some definitions and notations on the cotangent bundle.

    We say that a one-form to be horizontal (resp. vertical) if it vanishes on the vertical bundle \mathcal{V} (resp. on the horizontal bundle \mathcal{H}). We thus have a splitting of the cotangent space

    T^*_x \mathbb M= \mathcal{H}^*(x) \oplus \mathcal{V}^*(x)

    The metric g_\varepsilon induces then a metric on the cotangent bundle which we still denote g_\varepsilon. By using similar notations and conventions as before we have for every \eta in T^*_x \mathbb M,

    \| \eta \|^2_{\varepsilon} =\| \eta \|_\mathcal{H}^2+\varepsilon \| \eta \|_\mathcal{V}^2.

    By using the duality given by the metric g, (1,1) tensors can also be seen as linear maps on the cotangent bundle T^* \mathbb M. More precisely, if A is a (1,1) tensor, we will still denote by A the fiberwise linear map on the cotangent bundle which is defined as the g-adjoint of the dual map of A. The same convention will be made for any (r,s) tensor.

    We define then the horizontal Ricci curvature \mathfrak{Ric}_{\mathcal{H}} as the fiberwise symmetric linear map on one-forms such that for every smooth functions f,g,

    \langle \mathfrak{Ric}_{\mathcal{H}} (df), dg \rangle=\mathbf{Ricci} (\nabla_\mathcal{H} f ,\nabla_\mathcal{H} g),

    where \mathbf{Ricci} is the Ricci curvature of the connection \nabla.

    If V is a horizontal vector field and \varepsilon > 0, we consider the fiberwise linear map from the space of one-forms into itself which is given for \eta \in \Gamma^\infty(T^* \mathbb M) and Y \in \Gamma^\infty(T \mathbb M) by

    \mathfrak{T}^\varepsilon_V \eta (Y) = \begin{cases} \frac{1}{\varepsilon} \eta (J_Y V), \quad Y \in \Gamma^\infty(\mathcal{V}) \\ -\eta (T(V,Y)), Y \in \Gamma^\infty(\mathcal{H}) \end{cases}

    We observe that \mathfrak{T}^\varepsilon_V is skew-symmetric for the metric g_\varepsilon so that \nabla -\mathfrak{T}^\varepsilon is a g_\varepsilon-metric connection.

    If \eta is a one-form, we define the horizontal gradient of \eta in a local frame as the (0,2) tensor

    \nabla_\mathcal{H} \eta =\sum_{i=1}^n \nabla_{X_i} \eta \otimes \theta_i.

    We denote by \nabla_\mathcal{H}^\# \eta the symmetrization of \nabla_\mathcal{H} \eta .

    Similarly, we will use the notation

    \mathfrak{T}^\varepsilon_\mathcal{H} \eta =\sum_{i=1}^n \mathfrak{T}^\varepsilon_{X_i} \eta \otimes \theta_i.

    Finally, we will still denote by \Delta_{\mathcal{H}} the covariant extension on one-forms of the horizontal Laplacian. In a local horizontal frame, we have thus

    \Delta_\mathcal{H}=-\nabla_\mathcal{H}^* \nabla_\mathcal{H}=\sum_{i=1}^n \nabla_{X_i}\nabla_{X_i} -\nabla_{\nabla_{X_i} X_i}.

    For \varepsilon > 0, we consider the following operator which is defined on one-forms by

    \square_\varepsilon=-(\nabla_\mathcal{H} -\mathfrak{T}_\mathcal{H}^\varepsilon)^* (\nabla_\mathcal{H} -\mathfrak{T}_\mathcal{H}^\varepsilon)-\frac{1}{ \varepsilon}\mathbf{J}^2+\frac{1}{\varepsilon} \delta_\mathcal{H} T- \mathfrak{Ric}_{\mathcal{H}},

    where the adjoint is understood with respect to the metric g_{\varepsilon}. It is easily seen that, in a local horizontal frame,

    -(\nabla_\mathcal{H} -\mathfrak{T}_\mathcal{H}^\varepsilon)^* (\nabla_\mathcal{H} -\mathfrak{T}_\mathcal{H}^\varepsilon) =\sum_{i=1}^n (\nabla_{X_i} -\mathfrak{T}^\varepsilon_{X_i})^2 - ( \nabla_{\nabla_{X_i} X_i}- \mathfrak{T}^\varepsilon_{\nabla_{X_i} X_i}),

    Observe that if the foliation is of Yang-Mills type then

    \square_\varepsilon=-(\nabla_\mathcal{H} -\mathfrak{T}_\mathcal{H}^\varepsilon)^* (\nabla_\mathcal{H} -\mathfrak{T}_\mathcal{H}^\varepsilon)-\frac{1}{ \varepsilon}\mathbf{J}^2- \mathfrak{Ric}_{\mathcal{H}}.

    As a consequence, in the Yang-Mills case the operator \square_\varepsilon is seen to be symmetric for the metric g_\varepsilon.

    Theorem: For every f \in C^\infty(\mathbb M), we have

    d \Delta_{\mathcal{H}} f=\square_\varepsilon df.

    Proof: We only sketch the proof and refer to this paper for the details. If Z_1,\cdots,Z_m is a local vertical frame of the leaves, we denote

    \mathbf J(\eta)=\sum_{l=1}^mJ_{Z_l}(\iota_{Z_l}d\eta_\mathcal V),

    where \eta_\mathcal V is the the projection of \eta to the vertical cotangent bundle. It does not depend on the choice of the frame and therefore defines a globally defined tensor.
    Also, let us consider the map \mathcal{T} \colon \Gamma^\infty(\wedge^2 T^*\mathbb M)\to \Gamma^\infty( T^*\mathbb M) which is given in a local coframe \theta_i \in \Gamma^\infty(\mathcal{H}^*), \nu_k \in \Gamma^\infty(\mathcal{V}^*)

    \mathcal{T}(\theta_i\wedge\theta_j)=-\gamma_{ij}^l\nu_l,\quad \mathcal{T}(\theta_i\wedge\nu_k)=\mathcal{T}(\nu_k\wedge\nu_l)=0.

    A direct computation shows then that

    -(\nabla_\mathcal{H} -\mathfrak{T}_\mathcal{H}^\varepsilon)^* (\nabla_\mathcal{H} -\mathfrak{T}_\mathcal{H}^\varepsilon) = \Delta_{\mathcal{H}} +2\mathbf{J}-\frac{2}{\varepsilon}\mathcal{T}\circ d+\delta_\mathcal{H} T^*-\frac{1}{\varepsilon}\delta_\mathcal{H} T+\frac{1}{\varepsilon}\mathbf{J}^2.

    Thus, we just need to prove that if \square_\infty is the operator defined on one-forms by

    \square_\infty=\Delta_{\mathcal{H}}+2\mathbf J-\mathbf{Ric}_\mathcal{H}+\delta_\mathcal{H} T^* ,

    then for any f\in C^\infty(\mathbb M),

    d\Delta_\mathcal{H} f=\square_\infty df.

    A computation in local frame shows that

    d\Delta_{\mathcal{H}} f - \Delta_{\mathcal{H}} df = 2\mathbf{J}(df) -\mathbf{Ric}_\mathcal{H} (df) +\delta_\mathcal{H} T^* (df),

    which completes the proof \square

    We also can prove the following Bochner’s type identity whose proof can be found in the paper.

    Theorem: For any \eta \in \Gamma^\infty(T^* \mathbb M),

    \frac{1}{2} \Delta_{\mathcal{H}} \| \eta \|_{\varepsilon}^2 -\langle \square_\varepsilon \eta , \eta \rangle_{\varepsilon} = \| \nabla_{\mathcal{H}} \eta -\mathfrak{T}^\varepsilon_{\mathcal{H}} \eta \|_{\varepsilon}^2 + \left\langle \mathfrak{Ric}_{\mathcal{H}} (\eta), \eta \right\rangle_\mathcal{H} -\left \langle \delta_\mathcal{H} T (\eta) , \eta \right\rangle_\mathcal{V} +\frac{1}{\varepsilon} \langle \mathbf{J}^2 (\eta) , \eta \rangle_\mathcal{H}.

    Posted in Hypoelliptic operators | Leave a comment

    Lecture 2. Riemannian foliations. Model spaces

    Posted on October 6, 2014 by Fabrice Baudoin

    In this lecture, we first quickly review what was done in the previous one.  We then introduce the horizontal and vertical Laplacians and prove basic commutations results. We explain them the notion of Riemannian foliation. In the second part of the lecture we study the Heisenberg group and show how to compute its heat kernel.

    Let \pi: (\mathbb M , g)\to (\mathbb B,j) be a Riemannian submersion. If f \in C^\infty(\mathbb M) we define its vertical gradient \nabla_{\mathcal{V}} as the projection of its gradient onto the vertical distribution and its horizontal gradient \nabla_{\mathcal{H}} as the projection of the gradient onto the horizontal distribution. We define then the vertical Laplacian \Delta_{\mathcal{V}} as the generator of the Dirichlet form

    \mathcal{E}_{\mathcal{V}}(f,g)=-\int_{\mathbb M} \langle \nabla_{\mathcal{V}} f , \nabla_{\mathcal{V}} g \rangle d\mu
    where \mu is the Riemannian volume measure on \mathbb M. Similarly, we define the horizonal Laplacian \Delta_{\mathcal{H}} as the generator of the Dirichlet form

    \mathcal{E}_{\mathcal{H}}(f,g)=-\int_{\mathbb M} \langle \nabla_{\mathcal{H}} f , \nabla_{\mathcal{V}} g \rangle d\mu.
    If X_1,\cdots,X_n is a local orthonormal frame of basic vector fields and Z_1,\cdots,Z_m a local orthonormal frame of the vertical distribution, then we have

    \Delta_{\mathcal{H}}=-\sum_{i=1}^n X_i^* X_i
    and

    \Delta_{\mathcal{V}}=-\sum_{i=1}^m Z_i^* Z_i,
    where the adjoints are understood in L^2(\mu). Classically, we have

    X_i^*=-X_i+\sum_{k=1}^n \langle D_{X_k} X_k, X_i\rangle +\sum_{k=1}^m \langle D_{Z_k} Z_k, X_i\rangle,
    where D is the Levi-Civita connection. As a consequence, we obtain

    \Delta_{\mathcal{H}}=\sum_{i=1}^n X_i^2 -\sum_{i=1}^n (D_{X_i}X_i)_{\mathcal{H}} -\sum_{i=1}^m (D_{Z_i}Z_i)_{\mathcal{H}},
    where (\cdot)_{\mathcal{H}} denotes the horizontal part of the vector. In a similar way we obviously have

    \Delta_{\mathcal{V}}=\sum_{i=1}^m Z_i^2 -\sum_{i=1}^n (D_{X_i}X_i)_{\mathcal{V}} -\sum_{i=1}^m (D_{Z_i}Z_i)_{\mathcal{V}}.
    We can observe that the Laplace-Beltrami operator \Delta of \mathbb M can be written

    \Delta=\Delta_{\mathcal{H}}+\Delta_{\mathcal{V}}.
    It is worth noting that, in general, \Delta_{\mathcal{H}} is not the lift of the Laplace-Beltrami operator \Delta_\mathbb{B} on \mathbb B. Indeed, let us denote by \overline{X}_1,\cdots,\overline{X}_n the vector fields on \mathbb B which are \pi-related to X_1,\cdots,X_n .

    We have
    \Delta_{\mathbb B}=\sum_{i=1}^n \overline{X}_i^2 -\sum_{i=1}^n D_{\overline{X}_i}\overline{X}_i.
    Since it is easy to check that D_{\overline{X}_i}\overline{X}_i is \pi-related to (D_{X_i}X_i)_{\mathcal{H}}, we deduce that \Delta_{\mathcal{H}} lies above \Delta_{\mathbb B}, i.e. for every f \in C^\infty(\mathbb B), \Delta_{\mathcal{H}} (f \circ \pi)=(\Delta_{\mathbb B} f )\circ \pi , if and only if the vector

    T=\sum_{i=1}^m D_{Z_i}Z_i
    is vertical. This condition is equivalent to the fact that the mean curvature of each fiber is zero, or in other words that the fibers are minimal submanifolds of \mathbb M. This happens for instance for submersions with totally geodesic fibers.

    We also note that from Hormander’s theorem, the operator \Delta_{\mathcal{H}} is subelliptic if the horizontal distribution is bracket generating. Of course, the vertical Laplacian is never subelliptic because the vertical distribution is always integrable.

    The following result, though simple, will turn out to be extremely useful in the sequel when dealing with curvature dimension estimates and functional inequalities.

    Theorem:  The Riemannian submersion \pi has totally geodesic fibers if and only if for every f \in C^\infty(\mathbb M),
    \langle \nabla_{\mathcal{H}} f , \nabla_{\mathcal{H}} \| \nabla_{\mathcal{V}} f \|^2 \rangle=\langle \nabla_{\mathcal{V}} f , \nabla_{\mathcal{V}} \| \nabla_{\mathcal{H}} f \|^2 \rangle

    Proof: If X_1,\cdots,X_n is a local orthonormal frame of basic vector fields and Z_1,\cdots,Z_m a local orthonormal frame of the vertical distribution, then we easily compute that

    \langle \nabla_{\mathcal{H}} f , \nabla_{\mathcal{H}} \| \nabla_{\mathcal{V}} f \|^2 \rangle-\langle \nabla_{\mathcal{V}} f , \nabla_{\mathcal{V}} \| \nabla_{\mathcal{H}} f \|^2 \rangle=2\sum_{i=1}^n \sum_{j=1}^m (X_i f) (Z_j f) ([X_i,Z_j] f).

    As a consequence,

    \langle \nabla_{\mathcal{H}} f , \nabla_{\mathcal{H}} \| \nabla_{\mathcal{V}} f \|^2 \rangle=\langle \nabla_{\mathcal{V}} f , \nabla_{\mathcal{V}} \| \nabla_{\mathcal{H}} f \|^2 \rangle
    if and only if for every basic vector field X,

    \sum_{j=1}^m (Z_j f) ([X,Z_j] f)=0.
    This condition is equivalent to the fact that the flow generated by X induces an isometry between the fibers, and so from Hermann’s Theorem this is equivalent to the fact that the fibers are totally geodesic \square

    The second commutation result that characterizes totally geodesic submersions is due to Berard-Bergery and Bourguignon.

    Theorem: The Riemannian submersion \pi has totally geodesic fibers if and only if any basic vector field X commutes with the vertical Laplacian \Delta_{\mathcal{V}}. In particular, if \pi has totally geodesic fibers, then for every f \in C^\infty(\mathbb M),

    \Delta_{\mathcal{H}} \Delta_{\mathcal{V}} f=\Delta_{\mathcal{V}} \Delta_{\mathcal{H}} f.

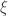    Proof. Assume that the submersion is totally geodesic. Let X be a basic vector field and \xi_t be the flow it generates. Since \xi induces an isometry between the fibers, we have

    \xi_t^* ( \Delta_{\mathcal{V}})= \Delta_{\mathcal{V}}.
    Differentiating at 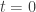t=0 yields [X,\Delta_{\mathcal{V}}]=0.

    Conversely, assume that for every basic field X, [X,\Delta_{\mathcal{V}}]=0. Let X_1,\cdots,X_n be a local orthonormal frame of basic vector fields and Z_1,\cdots,Z_m be a local orthonormal frame of the vertical distribution. The second order part of the operator [X,\Delta_{\mathcal{V}}] must be zero. Given the expression of the vertical Laplacian, this implies

    \sum_{i=1}^m [X,Z_i] Z_i=0.
    So X leaves the symbol of \Delta_{\mathcal{V}} invariant which is the metric on the vertical distribution. This implies that the flow generated by X induces isometries between the fibers.

    Finally, as we have seen, if the submersion is totally geodesic then in a local basic orthornomal frame

    \Delta_{\mathcal{H}}=\sum_{i=1}^n X_i^2 -\sum_{i=1}^n (D_{X_i}X_i)_{\mathcal{H}}.
    Since the vectors (D_{X_i}X_i)_{\mathcal{H}} are basic, from the previous result \Delta_{\mathcal{H}} commutes with \Delta_{\mathcal{V}} \square

    We now turn to the notion of Riemannian foliation.

    In many interesting cases, we do not actually have a globally defined Riemannian sumersion but a Riemannian foliation.

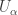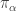    Definition:  Let \mathbb M be a smooth and connected n+m dimensional manifold. A m-dimensional foliation \mathcal{F} on \mathbb M is defined by a maximal collection of pairs \{ (U_\alpha, \pi_\alpha), \alpha \in I \} of open subsets U_\alpha of \mathbb M and submersions \pi_\alpha: U_\alpha \to U_\alpha^0 onto open subsets of \mathbb{R}^n satisfying:

    • \cup_{\alpha \in I} U_\alpha =\mathbb M;
    •  If U_\alpha \cap U_\beta \neq \emptyset, there exists a local diffeomorphism \Psi_{\alpha \beta} of \mathbb{R}^n such that \pi_\alpha=\Psi_{\alpha \beta} \pi_\beta on U_\alpha \cap U_\beta .

    The maps \pi_\alpha are called disintegrating maps of \mathcal{F}. The connected components of the sets \pi_\alpha^{-1}(c), c \in \mathbb{R}^n, are called the plaques of the foliation. A foliation arises from an integrable sub-bundle of T\mathbb M, to be denoted by 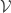\mathcal{V} and referred to as the vertical distribution. 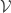These are the vectors tangent to the leaves, the maximal integral sub-manifolds of \mathcal{V}.

    Foliations have been extensively studied and numerous books are devoted to them. We refer in particular to the book by Tondeur.

    In the sequel, we shall only be interested in Riemannian foliations with bundle like metric.

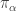    Definition: Let \mathbb M be a smooth and connected $mathbb n+m$ dimensional Riemannian manifold. A m-dimensional foliation \mathcal{F} on \mathbb M is said to be Riemannian with a bundle like metric if the disintegrating maps \pi_\alpha are Riemannian submersions onto U_\alpha^0 with its given Riemannian structure. If moreover the leaves are totally geodesic sub-manifolds of \mathbb M, then we say that the Riemannian foliation is totally geodesic with a bundle like metric.

    Observe that if we have a Riemannian submersion \pi : (\mathbb M,g) \to (\mathbb{B},j), then \mathbb M is equipped with a Riemannian foliation with bundle like metric whose leaves are the fibers of the submersion. Of course, there are many Riemannian foliations with bundle like metric that do not come from a Riemannian submersion.

    Since Riemannian foliations with a bundle like metric can locally be desribed by a Riemannian submersion, we can define a horizontal Laplacian \Delta_\mathcal{H} and a vertical Laplacian \Delta_\mathcal{V}. Observe that they commute on smooth functions if the foliation is totally geodesic. More generally all the local properties of a Riemannian submersion extend to Riemannian foliations.

     

    In the second part of the lecture, we deal with model spaces.

    One of the simplest non trivial Riemannian submersions with totally geodesic fibers and bracket generating horizontal distribution is associated to the Heisenberg group. The Heisenberg group is the set

    \mathbb{H}^{2n+1}=\left\{ (x,y,z), x \in \mathbb{R}^n, y \in \mathbb{R}^n, z\in\mathbb{R} \right\}
    endowed with the group law

    (x_1,y_1,z_1) \star (x_2,y_2,z_2)=(x_1+x_2,y_1+y_2,z_1+z_2+\langle x_1,y_2 \rangle_{\mathbb R^n} -\langle x_2,y_1 \rangle_{\mathbb R^n}).

    The vector fields

    X_i=\frac{\partial}{\partial x_i} -y_i \frac{\partial}{\partial z}
    Y_i=\frac{\partial}{\partial y_i} +x_i \frac{\partial}{\partial z}
    and

    Z=\frac{\partial}{\partial z}
    form an orthonormal frame of left invariant vector fields for the left invariant metric on \mathbb{H}^{2n+1}. Note that the following commutations hold

    [X_i,Y_j]=2\delta_{ij} Z, \quad [X_i,Z]=[Y_i,Z]=0.
    The map
    \pi : \begin{array}{lll} \mathbb{H}^{2n+1} &\to& \mathbb{R}^{2n} \\ (x,y,z) & \to & (x,y) \end{array}
    is then a Riemannian submersion with totally geodesic fibers. The horizontal Laplacian is the left invariant operator

    \Delta_{\mathcal{H}} =\sum_{i=1}^n (X_i^2+Y_i^2)

    =\sum_{i=1}^n \frac{\partial^2}{\partial x^2_i} +\frac{\partial^2}{\partial y^2_i} + 2\sum_{i=1}^n \left( x_i \frac{\partial}{\partial y_i}-y_i \frac{\partial}{\partial x_i}\right) \frac{\partial}{\partial z}+ (\| x\|^2+\| y \|^2) \frac{\partial^2}{\partial z^2}
    and the vertical Laplacian is the left invariant operator

    \Delta_\mathcal{V}=\frac{\partial^2}{\partial z^2} .
    The horizontal distribution

    \mathcal{H}=\mathbf{span} \{X_1, \cdots,X_n,Y_1,\cdots, Y_n\}
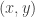    is bracket generating at every point, so \Delta_{\mathcal{H}} is a subelliptic operator. The operator \Delta_{\mathcal{H}} is invariant by the action of the orthogonal group of \mathbb{R}^{2n} on the variables (x,y). Introducing the variable r^2=\| x\|^2 +\|y\|^2, we see then that the radial part of \Delta_{\mathcal{H}} is given by

    \overline{\Delta}_{\mathcal{H}}=\frac{\partial^2}{\partial r^2}+\frac{2n-1}{r} \frac{\partial}{\partial r} +r^2 \frac{\partial^2}{\partial z^2}.
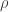    This means that if f: \mathbb{R}_{\ge 0} \times \mathbb R \to \mathbb R is a smooth map and \rho is the submersion (x,y,z)\to (\sqrt{\| x\|^2+\|y\|^2},z) then

    \Delta_{\mathcal{H}} (f \circ \rho)=(\overline{\Delta}_{\mathcal{H}} f) \circ \rho.
    From this invariance property in order to study the heat kernel and fundamental solution of \Delta_{\mathcal{H}}  at 0 it suffices to study the heat kernel and the fundamental solution of \overline{\Delta}_{\mathcal{H}} at 0.

    We denote by \overline{p}_t(r,z) the heat kernel at 0 of \overline{\Delta}_{\mathcal{H}}. It was first computed explicitly by Gaveau  building on previous works by Paul Levy.

    Proposition: For 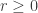r \ge 0 and z \in \mathbb{R},

    \overline{p}_t (r,z)=\frac{1}{(2\pi)^{n+1}} \int_\mathbb R e^{i \lambda z} \left( \frac{\lambda}{\sinh (2\lambda t)} \right)^n e^{-\frac{\lambda r^2}{ 2} \coth (2\lambda t) } d\lambda

    Proof: Since \frac{\partial}{\partial z} commutes with \overline{\Delta}_{\mathcal{H}}, the idea is to use a Fourier transform in z. We see then that

    \overline{p}_t(r,z)=\frac{1}{2\pi} \int_{\mathbb R} e^{i \lambda z} \Phi_t (r,\lambda) d\lambda,
    where \Phi_t (r,z,\lambda) is the fundamental solution at 0 of the parabolic partial differential equation

    \frac{\partial \Phi}{ \partial t}=\frac{\partial^2 \Phi }{\partial r^2}+\frac{2n-1}{r} \frac{\partial \Phi }{\partial r} -\lambda^2 r^2 \Phi .

    We thus want to compute the semigroup generated by the Schrodinger operator

    \mathcal{L}_\lambda=\frac{\partial^2 }{\partial r^2}+\frac{2n-1}{r} \frac{\partial }{\partial r} -\lambda^2 r^2.
    The trick is now to observe that for every f,

    \mathcal{L}_\lambda \left( e^{\frac{\lambda r^2}{2}} f \right)= e^{\frac{\lambda r^2}{2}} \left( 2n\lambda +\mathcal{G}_\lambda \right)f,
    where

    \mathcal{G}_\lambda=\frac{\partial^2 }{\partial r^2}+\left( 2 \lambda r+\frac{2n-1}{r} \right)\frac{\partial }{\partial r}.
    The operator \mathcal{G}_\lambda turns out to be the radial part of the Ornstein-Uhlenbeck operator \Delta_{\mathbb{R}^{2n}} +2 \lambda \langle x , \nabla_{\mathbb{R}^{2n}} \rangle whose heat kernel at 0 is a Gaussian density with mean 0 and variance \frac{1}{2\lambda}(e^{4\lambda t}-1). This means that the heat kernel at 0 of \mathcal{G}_\lambda is given by

    q_t (r)=\frac{1}{(2\pi)^{n}} \left( \frac{2\lambda}{e^{4\lambda t}-1} \right)^n e^{-\frac{\lambda r^2}{ e^{4\lambda t}-1}}.
    We conclude

    \Phi_t (r,z,\lambda)=\frac{e^{2n\lambda t}}{(2\pi)^n} \left( \frac{2\lambda}{e^{4\lambda t}-1} \right)^n e^{-\frac{\lambda r^2}{2}} e^{-\frac{\lambda r^2}{ e^{4\lambda t}-1}}

    \square

    The second simplest and geometrically relevant example is given by the celebrated Hopf fibration. Let us consider the odd dimensional unit sphere

    \mathbb{S}^{2n+1}=\lbrace z=(z_1,\cdots,z_{n+1})\in \mathbb{C}^{n+1}, \| z \| =1\rbrace.
    There is an isometric group action of \mathbb{S}^1=\mathbf{U}(1) on \mathbb{S}^{2n+1} which is defined by

    (z_1,\cdots, z_n) \rightarrow (e^{i\theta} z_1,\cdots, e^{i\theta} z_n).

    The generator of this action shall be denoted by T. We thus have for every f \in C^\infty(\mathbb S^{2n+1})

    Tf(z)=\frac{d}{d\theta}f(e^{i\theta}z)\mid_{\theta=0},
    so that

    T=i\sum_{j=1}^{n+1}\left(z_j\frac{\partial}{\partial z_j}-\overline{z_j}\frac{\partial}{\partial \overline{z_j}}\right).
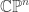    The quotient space \mathbb S^{2n+1} / \mathbf{U}(1) is the projective complex space \mathbb{CP}^n and the projection map \pi : \mathbb S^{2n+1} \to \mathbb{CP}^n is a Riemannian submersion with totally geodesic fibers isometric to \mathbf{U}(1). The fibration

    \mathbf{U}(1) \to \mathbb S^{2n+1} \to \mathbb{CP}^n

    is called the Hopf fibration.

     

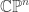    To study the geometry of the Hopf fibration, in particular the horizontal Laplacian \Delta_\mathcal{H}, it is convenient to introduce a set of coordinates that reflects the action of the isometry group of \mathbb{CP}^n on \mathbb{S}^{2n+1}.
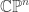    Let (w_1,\cdots, w_n,\theta) be the local inhomogeneous coordinates for \mathbb{CP}^n given by w_j=z_j/z_{n+1}, and \theta be the local fiber coordinate. i.e., (w_1, \cdots, w_n) parametrizes the complex lines passing through the north pole, while \theta determines a point on the line that is of unit distance from the north pole. More explicitly, these coordinates are given by the map

    (w,\theta)\longrightarrow \left(w e^{i\theta}\cos r ,e^{i\theta}\cos r \right),
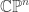    where r=\arctan \sqrt{\sum_{j=1}^{n}|w_j|^2} \in [0,\pi /2), \theta \in \mathbb R/2\pi\mathbb{Z}, and w \in \mathbb{CP}^n. In these coordinates, it is clear that T=\frac{\partial}{\partial \theta} and that the vertical Laplacian is

    \Delta_\mathcal{V}=\frac{\partial^2 }{\partial \theta^2}.
    Our first  goal is now to compute the horizontal Laplacian \Delta_\mathcal{H}. This operator is invariant by the action on the variables (w_1,\cdots,w_n) of the group of isometries of \mathbb{CP}^n that fix the north pole of \mathbb{S}^{2n+1} (this group is \mathbf{SU}(n)). Therefore the heat kernel at the north pole only depends on the variables (r,\theta).

    Proposition:  The radial part of the horizontal Laplacian is the operator

    \frac{\partial^2}{\partial r^2}+((2n-1)\cot r-\tan r)\frac{\partial}{\partial r}+\tan^2r\frac{\partial^2}{\partial \theta^2}

    Proof: The easiest route is to compute first the radial part of the Laplace-Beltrami operator \Delta and then to use the formula

    \Delta_\mathcal{H}=\Delta-\Delta_\mathcal{V}=\Delta-\frac{\partial}{\partial \theta^2}.
    In our parametrization of \mathbb{S}^{2n+1} we have,

    z_{n+1}=e^{i\theta}\cos r.
    Therefore if 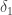\delta_1 denotes the Riemannian distance based at the north pole, we have \cos \delta_1 =\cos r \cos \theta and if \delta_2 denotes the Riemannian distance based at the point with real coordinates (0,\cdots,0,1) then we have \cos \delta_2=\cos r \sin \theta. 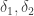The formula for the Laplace-Beltrami operator acting on functions depending on the Riemannian distance based at a point is well-known and we deduce from it that \Delta acts on functions depending only on \delta_1,\delta_2 as

    \frac{\partial^2}{\partial \delta_1^2} + 2n \cot \delta_1 \frac{\partial }{\partial \delta_1} +\frac{\partial^2}{\partial \delta_2^2} + 2n \cot \delta_2 \frac{\partial }{\partial \delta_2}
    In the variables (r,\theta) this last operator writes

    \frac{\partial^2}{\partial r^2}+((2n-1)\cot r-\tan r)\frac{\partial}{\partial r}+\frac{1}{\cos^2 r}\frac{\partial^2}{\partial \theta^2}.

    This concludes the proof \square

     

    Posted in Hypoelliptic operators | Leave a comment

    Lecture 1. Introduction and Riemannian submersions

    Posted on October 5, 2014 by Fabrice Baudoin

    ihp

    In this first lecture, I give a general introduction about the plan of the lectures and the materials to be covered and start with the study of Riemannian submersions. Thanks to  Ugo Boscain, the videos of the lectures are available and I greatly thank him for that.

     

    It is a fact that many interesting hypoelliptic diffusion operators may be studied by introducing a well-chosen Riemannian foliation. In particular, several sub-Laplacians on sub-Riemannians manifolds often appear as horizontal Laplacians of a foliation and several of the Kolmogorov type hypoelliptic diffusion operators which are used in the theory of kinetic equations appear as the sum of the vertical Laplacian of a foliation and of a first order term.

    The goal of the lectures is to survey some geometric analysis tools to study this kind of diffusion operators. We specially would like to stress the importance of subelliptic Bochner’s type identities in this framework and show how they can be used to deduce a variety of results ranging from topological informations on a sub-Riemannian manifold to hypocoercive estimates and convergence to equilibrium for kinetic Fokker-Planck equations. As an illustration of those methods we  will give a proof of a sub-Riemannian Bonnet-Myers type compactness theorem and, in the last lecture, study a version of the Bakry-Emery criterion for Kolmogorov type operators.

    For the proof of the sub-Riemannian Bonnet-Myers theorem we will  adapt an approach developed in a joint program with Nicola Garofalo. The object of this program  has been to propose a generalized curvature dimension inequality that fits a number of interesting subelliptic situations including the ones considered in these lectures. While some of them will be discussed here, the numerous applications of the generalized curvature dimension inequality are beyond the scope of the lectures and we will only give the relevant pointers to the literature. We focus here more on the Bonnet-Myers theorem and the geometric framework in which this curvature-dimension estimate is available.

    The course will be  organized as follows.

    1. We introduce first  the concept of Riemannian foliation and define the horizontal and vertical Laplacians. Basic theorems like the Berard-Bergery-Bourguignon commutation theorem will be proved.
    2. We will study in details some examples of Riemannian foliations with totally geodesic leaves that can be seen as model spaces. Besides the Heisenberg group, these examples are associated to the Hopf fibrations on the sphere. We give explicit expressions for the radial parts of the horizontal and vertical Laplacians and for the horizontal heat kernels of these model spaces.
    3. We will prove a transverse Weitzenbock formula for the horizontal Laplacian of a Riemannian foliation with totally geodesic leaves. It is the main geometric analysis tool for the study of the horizontal Laplacian. As a first consequence of this Weitzenbock formula, we prove that if natural assumptions are satisfied, then the horizontal Laplacian satisfies the generalized curvature dimension inequality. As a second consequence, we will prove sharp lower bounds for the first eigenvalue of the horizontal Laplacian.
    4. We will introduce the horizontal semigroup of a Riemannian foliation with totally geodesic leaves and discuss fundamental questions like essential self-adjointness for the horizontal Laplacian and stochastic completeness. We also prove Li-Yau gradient bounds for this horizontal semigroup.
    5. By using semigroup methods, we will prove a sub-Riemannian Bonnet-Myers theorem in the context of Riemannian foliations with totally geodesic leaves.
    6. The last course will be an introduction to the analysis of hypoelliptic Kolmogorov type operators on Riemannian foliations. We mainly focus on the problem of convergence to equilibrium for the parabolic equation associated to the operator and on methods to prove hypocoercive estimates. The example of the kinetic Fokker-Planck equation is given as an illustration.

     

    Let (\mathbb{M} , g) and (\mathbb{B},j) be smooth and connected Riemannian manifolds.

    Definition:  A smooth surjective map \pi:(\mathbb{M} , g) \to(\mathbb{B},j) is called a Riemannian submersion if its derivative maps T_x\pi : T_x \mathbb{M} \to T_{\pi(x)} \mathbb{B} are orthogonal projections.

    Example: (Warped products) Let (\mathbb{M}_1 , g_1) and (\mathbb{M}_2 , g_2) be Riemannian manifolds and f be a smooth and positive function on \mathbb{M}_1. Then the first projection (\mathbb{M}_1 \times \mathbb{M}_2,g_1 \oplus f g_2) \to (\mathbb{M}_1, g_1) is a Riemannian submersion.

    Example: (Quotient by an isometric action) Let (\mathbb{M} , g) be a Riemannian manifold and \mathbb G be a closed subgroup of the isometry group of (\mathbb M , g). Assume that the projection map \pi from \mathbb M to the quotient space \mathbb M /\mathbb{G} is a smooth submersion. Then there exists a unique Riemannian metric j on \mathbb M /\mathbb{G} such that \pi is a Riemannian submersion.

    If \pi is a Riemannian submersion and b \in \mathbb B, the set \pi^{-1}(\{ b \}) is called a fiber.

    For x \in \mathbb{M}, \mathcal{V}_x =\mathbf{Ker} (T_x\pi) is called the vertical space at x. The orthogonal complement of \mathcal{H}_x shall be denoted \mathcal{H}_x and will be referred to as the horizontal space at x.

    We have an orthogonal decomposition

    T_x \mathbb M=\mathcal{H}_x \oplus \mathcal{V}_x

    and a corresponding splitting of the metric

    g=g_{\mathcal{H}} \oplus g_{\mathcal{V}}.
    The vertical distribution \mathcal V is of course integrable since it is the tangent distribution to the fibers, but the horizontal distribution is in general not integrable. Actually, in all the situations we will consider the horizontal distribution is everywhere bracket-generating in the sense that for every x \in \mathbb M, \mathbf{Lie} (\mathcal{H}) (x)=T_x \mathbb M. In that case it is natural to study the sub-Riemannian geometry of the triple (\mathbb M, \mathcal{H}, g_{\mathcal{H}}). As we will see, many interesting examples of sub-Riemannian structures arise in this framework and this is really the situation which is interesting for us.

    We shall mainly be interested in submersion with totally geodesic fibers.

    Definition: A Riemannian submersion \pi: (\mathbb M , g)\to (\mathbb B,j) is said to have totally geodesic fibers if for every b \in \mathbb B, the set \pi^{-1}(\{ b \}) is a totally geodesic submanifold of \mathbb M.

    Example: (Quotient by an isometric action) Let (\mathbb M , g) be a Riemannian manifold and \mathbb G be a closed one-dimensional subgroup of the isometry group of (\mathbb M , g) which is generated by a complete Killing vector field X. Assume that the projection map \pi from \mathbb M to \mathbb M /\mathbb{G} is a smooth submersion. Then the fibers are totally geodesic if and only if the integral curves of X are geodesics, which is the case if and only if X has a constant length.

    Example: (Principal bundle) Let \mathbb M be a principal bundle over \mathbb B with fiber \mathbf F and structure group \mathbb G. Then, given a Riemannian metric j on \mathbb B, a \mathbb G-invariant metric k on \mathbf{F} and a \mathbb G connection form \theta, there exists a unique Riemannian metric g on \mathbb M such that the bundle projection map \pi: \mathbb M \to \mathbb B is a Riemannian submersion with totally geodesic fibers isometric to (\mathbf{F},k) and such that the horizontal distribution of \theta is the orthogonal complement of the vertical distribution. In the case of the tangent bundle of a Riemannian manifold, the construction yields the Sasaki metric on the tangent bundle.

    As we will see, for a Riemannian submersion with totally geodesic fibers, all the fibers are isometric. The argument, due to Hermann  relies on the notion of basic vector field that we now introduce.

    Let \pi: (\mathbb M , g)\to (\mathbb B,j) be a Riemannian submersion. A vector field X \in \Gamma^\infty(T\mathbb M) is said to be projectable if there exists a smooth vector field \overline{X} on \mathbb B such that for every x \in \mathbb M, T_x \pi ( X(x))= \overline {X} (\pi (x)). In that case, we say that X and \overline{X} are \pi-related.

    Definition: A vector field X on \mathbb M is called basic if it is projectable and horizontal.

    If \overline{X} is a smooth vector field on \mathbb B, then there exists a unique basic vector field X on \mathbb M which is \pi-related to \overline{X}. This vector is called the lift of \overline{X}.

    Notice that if X is a basic vector field and Z is a vertical vector field, then T_x\pi ( [X,Z](x))=0 and thus [X,Z] is a vertical vector field. The following result is due to Hermann.

    Proposition: The submersion \pi has totally geodesic fibers if and only if the flow generated by any basic vector field induces an isometry between the fibers.

    Proof: We denote by D the Levi-Civita connection on \mathbb M. Let X be a basic vector field. If Z_1,Z_2 are vertical fields, the Lie derivative of g with respect to X can be computed as

    (\mathcal{L}_X g)(Z_1,Z_2)=\langle D_{Z_1} X ,Z_2 \rangle +\langle D_{Z_2} X ,Z_1 \rangle.
    Because X is orthogonal to Z_2, we now have \langle D_{Z_1} X ,Z_2 \rangle=-\langle X ,D_{Z_1} Z_2 \rangle. Similarly \langle D_{Z_2} X ,Z_1 \rangle=-\langle X ,D_{Z_2} Z_1 \rangle. We deduce

    (\mathcal{L}_X g)(Z_1,Z_2) =-\langle X ,D_{Z_1} Z_2 +D_{Z_2} Z_1 \rangle

    =-2 \langle X ,D_{Z_1} Z_2 \rangle.

    Thus the flow generated by any basic vector field induces an isometry between the fibers if and only if D_{Z_1} Z_2 is always vertical which is equivalent to the fact that the fibers are totally geodesic submanifolds.

    Posted in Hypoelliptic operators | Leave a comment

    Sub-Laplacians and hypoelliptic operators on totally geodesic Riemannian foliations

    Posted on September 1, 2014 by Fabrice Baudoin

    I finally finished the lecture notes of my course for the Institut Henri Poincare trimester Geometry, Analysis and Dynamics on sub-Riemannian manifolds. The course which is entitled Hypoelliptic operators is divided into two parts of each 12 hours. Nicola Garofalo will cover the first part of the course and I will cover the second one. In my part of the course, I will study sub-Laplacians and hypoelliptic operators on  Riemannian foliations with totally geodesic leaves.

    Here are the lecture notes: Cours IHP

    In 12 hours I may not have the time to cover all the parts of those notes but will try to focus on the main ideas and main results.

    Posted in Hypoelliptic operators | Leave a comment

    About the work of Martin Hairer

    Posted on August 12, 2014 by Fabrice Baudoin

    The 2014 Fields medals were awarded to Artur Avila, Manjul Bhargava, Martin Hairer and Maryam Mirzakhani. Their works are shortly described in the IMU announcement. Artur Avila main contributions are in ergodic theory and dynamical systems. Manjul Bhargava’s are in number theory. Martin Hairer’s are in stochastic analysis and Maryam Mirzakhani’s are in hyperbolic geometry.

    Maryam Mirzakhani is the first woman to receive the Fields medal. This is certainly an historic event and great news for a discipline in which men are traditionally overrepresented.

    In this short post, I would like to discuss, at a non-technical level, some ideas related to the beautiful works of Martin Hairer, whom I know since quite a long time and whose works are the most familiar to me among the medalists. Hairer’s recent results deal with the study of very rough random dynamical systems and build on ideas going back at least to Kiyoshi Ito which have been revisited more recently by Terry Lyons.

    Assume that we are interested in defining solutions for a differential equation that writes

    y(t)=y(0)+\int_0^t \sigma(y(s)) dx(s)

    where \sigma: \mathbb{R}^n \to \mathbb{R}^{n \times n} and x:[0,+\infty)\to \mathbb{R}^n is the driving path of the equation. If x and \sigma are regular enough, let us say smooth, then by using a fixed point argument, we can prove that the equation has a unique locally defined solution y. The integral \int_0^t \sigma(y(s)) dx(s) is then understood in the classical Riemann-Stieltjes sense.

    Assume now that we would like to understand what could be a solution of the same equation when x is not regular anymore, but  let us say has a bounded p-variation with p > 1. A natural idea is to consider a sequence x_n of smooth approximations of x, look at the equation

    y_n(t)=y(0)+\int_0^t \sigma(y_n(s)) dx_n(s)

    and hope for the best, which is the convergence of y_n to some y which would be universal, that is, independent from the actually approximating sequence x_n. This idea has been carried out in the 1990’s by Terry Lyons in his theory of rough paths (a set of lecture notes on the theory are available on the blog). A key insight is the correct topology in which we have to understand the statement x_n approximates x. Terry Lyons proved that this topology depends on the integer part of p. If 1 \le p <2, then it is enough that x_n\to x in the p-variation topology. If 2 \le p<3, it is not enough that x_n\to x, we also want the convergence in p-variation of the double integrals \int x^i_n dx^j_n. If 3\le p <4 we will also require a convergence in p-variation of the triple integrals, and so on and so forth. Thus, the topology that works is intimately related to the level of irregularity of the path x.

    Martin Hairer recently developed a theory of regularity structures that encompasses as a special case the rough paths theory of Terry Lyons and that somehow can be thought as an extension of Lyons’ ideas to the space variables . His theory allows to give a sense to solutions of extremely rough partial differential equations that naturally arise in mathematical physics. A primary example that Martin Hairer was able to deal with is the Kardar-Parisi-Zhang equation (in short KPZ) that I now shortly discuss. The (one-dimensional) KPZ equation writes

    \partial_t h =\partial_x^2 h + (\partial_x h)^2 -C+\xi

    where \xi is a white noise. From classical estimates, we expect h to look like a Brownian motion in space at any fixed time. The derivative \partial_x h is then a distribution, so the square of \partial_x h does not make sense !

    Similarly to the rough paths approach, Martin Hairer proves that if we consider a sequence of equations

    \partial_t h_\varepsilon =\partial_x^2 h_\varepsilon + (\partial_x h_\varepsilon)^2 -C_\varepsilon+\xi_\varepsilon

    where \xi_\varepsilon is smooth and converges in an appropriate sense to the white noise \xi and where C_\varepsilon is a well-chosen constant, then the solution h_\varepsilon converges to a limit which is universal. A key insight is to reduce the problem of the convergence of h_\varepsilon to the problem of the convergence of a finite set of “building blocks” of the approximation. By analogy with the rough paths theory, these building blocks may be thought as an analogue of the iterated integrals of the driving path. As in the rough paths case, the topology that works is intimately related to the level of irregularity of the noise \xi.

    The regularity structure of Martin Hairer applies far beyond the one-dimensional KPZ equation and proposes actually a general set of tools to explicitly construct good approximations given a singular equation. This is a revolutionary approach that offers a new look on several fundamental equations in mathematical physics that were long thought to be impossible to handle in a rigorous mathematical way.

    Here is the laudation of Hairer’s work by Ofer Zeitouni which is followed by Martin Hairer’s lecture.

    Posted in Mathematicians | Leave a comment