In this Lecture, we show how Sobolev inequalities on a Riemannian manifold are related to the volume growth of metric balls. The link between the Hardy-Littlewood-Sobolev theory and heat kernel upper bounds is due to Varopoulos, but the proof I give below I learnt it from my colleague Bañuelos. It bypasses the Marcinkiewicz interpolation theorem by using the Stein’s maximal ergodic lemma.
Let  be a complete Riemannian manifold and let
be a complete Riemannian manifold and let  be the Laplace-Beltrami operator of
be the Laplace-Beltrami operator of  . As usual, we denote by
. As usual, we denote by  the semigroup generated by
the semigroup generated by  and we assume
and we assume  .
.
We have the following so-called maximal ergodic lemma, which was first proved by Stein. We give here the probabilistic proof since it comes with a nice constant but you can find the original (non probabilistic) proof here.
Lemma:(Stein’s maximal ergodic theorem) Let  . For
. For  , denote
, denote  . We have
. We have

Proof: For  , we denote by
, we denote by  the Markov process with generator
the Markov process with generator  and started at
and started at  . We fix
. We fix  . By construction, for
. By construction, for  , we have,
, we have,

and thus

As a consequence, we obtain

Jensen’s inequality yields then

We deduce

Integrating the inequality with respect to the Riemannian measure  , we obtain
, we obtain

By reversibility, we get then

We now observe that the process  is martingale and thus Doob’s maximal inequality gives
is martingale and thus Doob’s maximal inequality gives

The proof is complete. 
We now turn to the theorem by Varopoulos.
Theorem: Let  ,
,  , and
, and  . If there exists
. If there exists  such that for every
such that for every 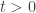 ,
,  ,
,

then for every  ,
,

Proof: We first observe that the bound

implies that  . Denote
. Denote  . We have
. We have

Pick  , to be later chosen, and split the integral in two parts:
, to be later chosen, and split the integral in two parts:

where  and
and  . We have
. We have

On the other hand,



We deduce

Optimizing the right hand side of the latter inequality with respect to  yields
yields

The proof is then completed by using Stein’s maximal ergodic theorem 
A special case, of particular interest, is when  and
and 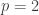 . We get in that case the following Sobolev inequality:
. We get in that case the following Sobolev inequality:
Theorem: Let 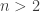 . If there exists
. If there exists  such that for every
such that for every 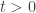 ,
,  ,
,

then for every  ,
,
 .
.
We mention that the constant in the above Sobolev inequality is not sharp even in the Euclidean case.
Combining the above with the Li-Yau upper bound for the heat kernel, we deduce the following theorem:
Theorem: Assume that  and that there exists a constant
and that there exists a constant  such that for every
such that for every  and
and 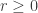 ,
,  , then there exists a constant
, then there exists a constant  such that for every
such that for every  ,
,

In many situations, heat kernel upper bounds with a polynomial decay are only available in small times the following result is thus useful:
Theorem: Let  ,
,  , and
, and  . If there exists
. If there exists  such that for every
such that for every  ,
,  ,
,

then, there is constant 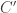 such that for every
such that for every  ,
,

Proof: We apply the Varopoulos theorem to the semigroup  . Details are let to the reader
. Details are let to the reader 
The following corollary shall be later used:
Corollary: Let 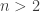 . If there exists
. If there exists  such that for every
such that for every  ,
,  ,
,

then there is constant 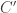 such that for every
such that for every  ,
,



