An important part of my research from the past few years has been to try to understand the notion of Ricci curvature lower bound in sub-Riemannian geometry. On this problem, my point of view is more the one of an analyst or even a probabilist than a geometer: My main device is a second order differential operator, a sub-Laplacian, and my main tools to understand global geometric properties are heat flow techniques. In sub-Riemannian geometry, this point of view can be fruitful in some aspects that I will describe now.
Although during the last three decades there have been several advances in the study of sub Riemannian spaces and the closely connected theory of sub-elliptic pde’s, most of the developments to date are of a local nature. As a consequence, the theory presently lacks a body of results which, similarly to the Riemannian case, connect properties of solutions of the relevant pde’s to the geometry of the ambient manifold. To illustrate this point, let me discuss some of the most fundamental local estimates concerning the subelliptic Hörmander‘s type operators.
Let  be a smooth and connected Riemannian manifold and
be a smooth and connected Riemannian manifold and  be a smooth measure on
be a smooth measure on  . Let us assume that there exists on
. Let us assume that there exists on  a family of vector fields
a family of vector fields  that satisfy the bracket generating condition. We are interested in the subelliptic operator
that satisfy the bracket generating condition. We are interested in the subelliptic operator  which is symmetric with respect to the measure
which is symmetric with respect to the measure  . In order to study
. In order to study  , the Riemannian distance
, the Riemannian distance 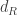 of
of  is most of the times confined to the background. There is another distance on
is most of the times confined to the background. There is another distance on  , that was introduced by Carathéodory, which plays a central role. A piecewise
, that was introduced by Carathéodory, which plays a central role. A piecewise 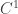 curve
curve ![\gamma:[0,T]\to \mathbb M](https://s0.wp.com/latex.php?latex=%5Cgamma%3A%5B0%2CT%5D%5Cto+%5Cmathbb+M&bg=ffffff&fg=333333&s=0&c=20201002) is called subunitary at
is called subunitary at  if for every
if for every  one has
one has  We define the subunit length of
We define the subunit length of  as
as  . If we indicate with
. If we indicate with 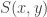 the family of subunit curves such that
the family of subunit curves such that  and
and  , then thanks to the fundamental accessibility theorem of Chow-Rashevsky the connectedness of
, then thanks to the fundamental accessibility theorem of Chow-Rashevsky the connectedness of  implies that
implies that  for every
for every  . This allows to define the sub-Riemannian distance on
. This allows to define the sub-Riemannian distance on  as follows
as follows 
Another elementary consequence of the Chow-Rashevsky theorem is that the identity map  is continuous and thus, the topologies of
is continuous and thus, the topologies of 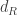 and
and  coincide. Several fundamental properties of the metric
coincide. Several fundamental properties of the metric  have been discussed in the seminal paper by Nagel, Stein and Wainger. In particular, the following result provides a uniform local control of the growth of the metric balls in
have been discussed in the seminal paper by Nagel, Stein and Wainger. In particular, the following result provides a uniform local control of the growth of the metric balls in  . It is known as the local doubling condition.
. It is known as the local doubling condition.
Theorem 1: For any  there exist constants
there exist constants  such that with
such that with  one has
one has

Moreover, given any compact set  one has
one has

This remarkable theorem is a fundamental local property of the metric space  and may be connected to several local estimates related to the operator
and may be connected to several local estimates related to the operator  . We mention in particular the Poincaré inequality on balls:
. We mention in particular the Poincaré inequality on balls:
Theorem 2: (D. Jerison) Let  and
and  . There exists a constant
. There exists a constant  such that for every
such that for every  and
and  ,
,

where  .
.
We stress again that these theorems and the methods to prove them are local in nature. This naturally raises the following question:
Question 1: Can we find conditions on the operator  ensuring that global versions of theorems like Theorems 1 and 2 hold true ?
ensuring that global versions of theorems like Theorems 1 and 2 hold true ?
By global versions of Theorems 1 and 2, we mean that the estimates should hold true on non necessarily compact manifolds and with constants uniformly controlled by the sub-Riemannian geometry of  . To find a way to tackle this question, let us first discuss what could be a satisfying answer in the simplest non trivial case: The case where
. To find a way to tackle this question, let us first discuss what could be a satisfying answer in the simplest non trivial case: The case where  is elliptic, that is
is elliptic, that is  form a basis of the tangent space at each point. In this case, there is a definite satisfying answer to Question 1: Global versions of the Theorems 1 and 2 may be obtained under the assumption that
form a basis of the tangent space at each point. In this case, there is a definite satisfying answer to Question 1: Global versions of the Theorems 1 and 2 may be obtained under the assumption that  satisfies a curvature dimension inequality.
satisfies a curvature dimension inequality.
The notion of curvature dimension inequality originates from the analysis of the Laplace-Beltrami operator on a Riemannian manifold and more precisely from the Bochner’s formula which states that if  is a Riemannian manifold with Laplacian
is a Riemannian manifold with Laplacian  , for any
, for any  one has
one has

Using the Cauchy-Schwarz inequality, which gives  , we thus see that the assumption that the Riemannian Ricci tensor on
, we thus see that the assumption that the Riemannian Ricci tensor on  be bounded from below by
be bounded from below by  implies
implies

What is remarkable is that this inequality perfectly captures the notion of Ricci lower bounds and dimensional upper bound: On a finite dimensional Riemannian manifold  the inequality is actually equivalent to Ric
the inequality is actually equivalent to Ric  and
and  .
.
This observation leads Bakry to define the notion of curvature dimension inequality for arbitrary second-order differential operators. Let  be, as before, a second order differential operator. Consider the following bilinear differential forms on functions
be, as before, a second order differential operator. Consider the following bilinear differential forms on functions  ,
,

and
![\Gamma_{2}(f,g) = \frac{1}{2}\big[L \Gamma(f,g) - \Gamma(f, L g)-\Gamma (g,L f)\big].](https://s0.wp.com/latex.php?latex=%5CGamma_%7B2%7D%28f%2Cg%29+%3D+%5Cfrac%7B1%7D%7B2%7D%5Cbig%5BL+%5CGamma%28f%2Cg%29+-+%5CGamma%28f%2C+L+g%29-%5CGamma+%28g%2CL+f%29%5Cbig%5D.&bg=ffffff&fg=333333&s=0&c=20201002)
When 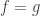 , we simply write
, we simply write  ,
,  . A straightforward computation shows that if, in a local chart,
. A straightforward computation shows that if, in a local chart,

then, in the same chart

As a consequence, for every smooth function  ,
,  The bilinear form
The bilinear form  is of second order and has no sign in general. We observe that if
is of second order and has no sign in general. We observe that if  is a Laplace-Beltrami operator, then Bochner’s formula writes
is a Laplace-Beltrami operator, then Bochner’s formula writes

Definition: The operator  is said to satisfy the curvature dimension inequality CD
is said to satisfy the curvature dimension inequality CD ,
,  ,
,  , if for every function
, if for every function  :
:

As we just pointed it out, if  is a Laplace-Beltrami operator, then it satisfies CD
is a Laplace-Beltrami operator, then it satisfies CD if and only if Ric
if and only if Ric  and
and  . But, what is interesting here is that the curvature dimension inequality may be satisfied without
. But, what is interesting here is that the curvature dimension inequality may be satisfied without  necessarily being a Laplace-Beltrami operator. In that case, the curvature dimension inequality is equivalent to a lower bound on the Bakry-Emery tensor of
necessarily being a Laplace-Beltrami operator. In that case, the curvature dimension inequality is equivalent to a lower bound on the Bakry-Emery tensor of  . We have then the following, a priori, satisfying answer to our Question 1:
. We have then the following, a priori, satisfying answer to our Question 1:
Fact: If  satisfies CD
satisfies CD , with
, with  and
and  , then we have global versions of Theorems 1 and 2.
, then we have global versions of Theorems 1 and 2.
More precisely, we have the following result:
Theorem: Let  be a subelliptic second order operator that satisfies CD
be a subelliptic second order operator that satisfies CD , with
, with  and
and  . Then, there exist constants
. Then, there exist constants  , depending only on
, depending only on 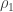 and
and  , for which one has for every
, for which one has for every  and every
and every 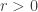 :
:

and

for every  .
.
Unfortunately, this fact only has a limited interest for us, since it is possible to prove that if a subelliptic operator  satisfies CD
satisfies CD , with
, with  and
and  , then
, then  is actually elliptic ! With this in mind, the next question that naturally arises is:
is actually elliptic ! With this in mind, the next question that naturally arises is:
Question 2: Is there an appropriate notion of curvature dimension inequality that applies to subelliptic operators ?
At this level of generality, this question certainly does not admit a definite satisfying answer. However with my co-author, N. Garofalo, we introduced a curvature dimension inequality that applies to a large class of subelliptic operators.
To introduce the relevant setting we consider a smooth, connected manifold  endowed with a smooth measure
endowed with a smooth measure  and a smooth, locally subelliptic, second order differential operator
and a smooth, locally subelliptic, second order differential operator  which is symmetric with respect to
which is symmetric with respect to  . As above, we associate with
. As above, we associate with  the following symmetric, first-order, differential bilinear form:
the following symmetric, first-order, differential bilinear form:

There is a genuine distance  canonically associated with
canonically associated with  which is continuous and defines the topology of
which is continuous and defines the topology of  . It is given by
. It is given by

We always assume that this distance is finite and that the metric space  is complete. This implies that
is complete. This implies that  is essentially self-adjoint.
is essentially self-adjoint.
We also suppose, and this is the main new ingredient, that we are given on  a symmetric, first-order differential bilinear form
a symmetric, first-order differential bilinear form  , satisfying
, satisfying

The following hypothesis on  plays a pervasive role in the results that we will describe and is natural in several geometric situations: For every
plays a pervasive role in the results that we will describe and is natural in several geometric situations: For every  , we have
, we have 
Before we proceed with the discussion, we pause to stress that, in the generality in which we work the bilinear differential form  , unlike
, unlike  , is not a priori intrinsic. Whereas
, is not a priori intrinsic. Whereas  is determined once
is determined once  is assigned, the form
is assigned, the form  in general is not intrinsically associated with
in general is not intrinsically associated with  . However, in several geometric examples the choice of
. However, in several geometric examples the choice of  will be natural and even canonical, up to a constant. This is the case, for instance, for one of the important geometric examples covered by our analysis: The CR Sasakian manifolds. Roughly speaking, we can think of
will be natural and even canonical, up to a constant. This is the case, for instance, for one of the important geometric examples covered by our analysis: The CR Sasakian manifolds. Roughly speaking, we can think of  as an orthogonal complement of
as an orthogonal complement of  : the bilinear form
: the bilinear form  represents the square of the length of the gradient in the horizontal directions, whereas
represents the square of the length of the gradient in the horizontal directions, whereas  represents the square of the length of the gradient along the vertical directions.
represents the square of the length of the gradient along the vertical directions.
Given the subelliptic operator  and the first-order bilinear forms
and the first-order bilinear forms  and
and  on
on  , we introduce the following second-order differential bilinear forms:
, we introduce the following second-order differential bilinear forms:
![\Gamma_{2}(f,g) = \frac{1}{2}\big[L\Gamma(f,g) - \Gamma(f, Lg)-\Gamma (g,Lf)\big],](https://s0.wp.com/latex.php?latex=%5CGamma_%7B2%7D%28f%2Cg%29+%3D+%5Cfrac%7B1%7D%7B2%7D%5Cbig%5BL%5CGamma%28f%2Cg%29+-+%5CGamma%28f%2C+Lg%29-%5CGamma+%28g%2CLf%29%5Cbig%5D%2C&bg=ffffff&fg=333333&s=0&c=20201002)
and
![\Gamma^Z_{2}(f,g) = \frac{1}{2}\big[L\Gamma^Z (f,g) - \Gamma^Z(f, Lg)-\Gamma^Z (g,Lf)\big].](https://s0.wp.com/latex.php?latex=%5CGamma%5EZ_%7B2%7D%28f%2Cg%29+%3D+%5Cfrac%7B1%7D%7B2%7D%5Cbig%5BL%5CGamma%5EZ+%28f%2Cg%29+-+%5CGamma%5EZ%28f%2C+Lg%29-%5CGamma%5EZ+%28g%2CLf%29%5Cbig%5D.&bg=ffffff&fg=333333&s=0&c=20201002)
Observe that if  , then
, then  as well. As for
as well. As for  and
and  , we will use the notations
, we will use the notations  ,
,  . The main definition and tool we proposed is the following:
. The main definition and tool we proposed is the following:
Definition: We say that the subelliptic operator  satisfies the generalized curvature-dimension inequality CD
satisfies the generalized curvature-dimension inequality CD if there exist constants
if there exist constants  ,
,  ,
,  , and
, and  such that the inequality
such that the inequality

holds for every  and every
and every 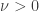 .
.
The motivation behind this definition comes from examples arising in geometry.
Theorem: Let  be a strictly pseudo convex CR manifold with real dimension
be a strictly pseudo convex CR manifold with real dimension 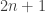 and vanishing Tanaka-Webster pseudohermitian torsion, i.e., a Sasakian manifold. The Tanaka-Webster Ricci tensor satisfies the lower bound
and vanishing Tanaka-Webster pseudohermitian torsion, i.e., a Sasakian manifold. The Tanaka-Webster Ricci tensor satisfies the lower bound

if and only if the CR sub-Laplacian of  satisfies the curvature-dimension inequality CD
satisfies the curvature-dimension inequality CD with
with  . Moreover, the hypothesis
. Moreover, the hypothesis  is satisfied.
is satisfied.
With this examples in mind let us now come back to the general framework and give a good answer to Question 1 in many purely subelliptic examples. In the following theorem that I proved with N. Garofalo and M. Bonnefont, the hypothesis  is supposed to be satisfied.
is supposed to be satisfied.
Theorem: Let  be a subelliptic second order operator that satisfies CD
be a subelliptic second order operator that satisfies CD , with
, with  ,
,  ,
,  and
and  . Then, there exist constants
. Then, there exist constants  , depending only on
, depending only on 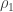 and
and  , for which one has for every
, for which one has for every  and every
and every 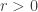 :
:

and

for every  .
.
Besides this result, the generalized curvature dimension inequality was also used to prove a Bonnet-Myers type theorem, the first of its kind in sub-Riemannian geometry.
The study of this generalized curvature dimension condition and of some of its extensions has generated quite a lot of research with my colleagues Michel Bonnefont, Nicola Garofalo, Isidro Munive and my students Bumsik Kim and Jing Wang.
-dimensional Riemannian manifold
with non negative Ricci curvature. The volume doubling property that was proved is closely related to sharp lower and upper Gaussian bounds that are due to P. Li and S.T. Yau. We first record a basic consequence of the volume doubling property whose proof is let to the reader.
be the constant such that for every
,
,
. Let
. For any
and
one has
there exists a constant
, which tends to
as
, such that for every
and
one has
,
, and every
,
from below. But this has already been done in the proof of the volume doubling property where we established:
, by the trivial inequality
, we conclude
, where
is the doubling constant.
, it is clear that we can choose
such that
is a constant which tends to
as
. The desired conclusion follows by suitably adjusting the values of both
and of the constant in the right-hand side of the estimate
with
. We encourage the reader to do the proof by herself/himself as an exercise.
with
. For any
there exist constants
, such that for every
and
one has
