In this section we shall consider a smooth and complete Riemannian manifold  with dimension
with dimension  . The Riemannian measure will be denoted by
. The Riemannian measure will be denoted by  .
.
The Laplace-Beltrami of  will be denoted by
will be denoted by  . Since
. Since  is assumed to be complete, as we have seen in the previous section, the operator
is assumed to be complete, as we have seen in the previous section, the operator  is essentially self-adjoint on the space
is essentially self-adjoint on the space  . More precisely, there exists an increasing sequence
. More precisely, there exists an increasing sequence  such that
such that  on
on  , and
, and  , as
, as 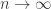 .
.
The Friedrichs extension of  , which is therefore the unique self-adjoint extension of
, which is therefore the unique self-adjoint extension of  in
in  will still be denoted by
will still be denoted by  and the domain of this extension is denoted by
and the domain of this extension is denoted by  .
.
We shall not repeat the whole theory of diffusion semigroups on manifolds, since many of the results that were proved before are easily extended to manifolds. In particular, we may prove:
- By using the spectral theorem for
 in the Hilbert space
in the Hilbert space  , we may construct a strongly continuous contraction semigroup
, we may construct a strongly continuous contraction semigroup  in
in  whose infinitesimal generator is
whose infinitesimal generator is  ;
;
- By using the ellipticity of
 , we may prove that
, we may prove that  admits a heat kernel, that is: There is a smooth function
admits a heat kernel, that is: There is a smooth function  ,
,  , such that for every
, such that for every  and
and  ,
,  Moreover, the heat kernel satisfies the two following conditions:
Moreover, the heat kernel satisfies the two following conditions:
- (Symmetry)
 ;
;
- (Chapman-Kolmogorov relation)
 .
.
- The semigroup
 is a sub-Markov semigroup: If
is a sub-Markov semigroup: If  is a function in
is a function in  , then
, then  .
.
- By using the Riesz-Thorin interpolation theorem,
 defines a contraction semigroup on
defines a contraction semigroup on  ,
,  .
.
Let us now assume that  is a compact Riemannian manifold. In that case, it obviously complete. As usual, we denote by
is a compact Riemannian manifold. In that case, it obviously complete. As usual, we denote by  the heat semigroup and by
the heat semigroup and by  the corresponding heat kernel. As a preliminary result, we have the following Liouville’s type theorem.
the corresponding heat kernel. As a preliminary result, we have the following Liouville’s type theorem.
Lemma: Let  such that
such that  , then
, then  is a constant function.
is a constant function.
Proof: From the ellipticity of  , we first deduce that
, we first deduce that  is smooth. Then, since
is smooth. Then, since  is compact, the following equality holds
is compact, the following equality holds  Therefore
Therefore  , which implies that
, which implies that  is a constant function
is a constant function 
In the compact case, the heat semigroup satisfies the so-called stochastic completeness (or Markov) property.
Proposition: For 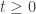 ,
, 
Proof: Since the constant function  is in
is in  , by compactness of
, by compactness of  , we may apply uniqueness of solutions of the heat equation in
, we may apply uniqueness of solutions of the heat equation in 

It turns out that the compactness of  implies the compactness of the semigroup.
implies the compactness of the semigroup.
Proposition: For 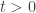 the operator
the operator  is a compact operator on the Hilbert space
is a compact operator on the Hilbert space  . It is moreover trace class and
. It is moreover trace class and 
Proof: We shall provide two proofs of the fact that  is a compact operator. You may observe that the first proof does not rely on the existence result of the heat kernel. The first proof stems from the local regularity theory of elliptic operators. Indeed, for
is a compact operator. You may observe that the first proof does not rely on the existence result of the heat kernel. The first proof stems from the local regularity theory of elliptic operators. Indeed, for 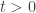 , the operator
, the operator  is bounded. Moreover, from Rellich’s theorem, the map
is bounded. Moreover, from Rellich’s theorem, the map  , is compact. Therefore by composition,
, is compact. Therefore by composition,
 is a compact operator.
is a compact operator.
The second proof is simpler and more direct. Indeed, from the existence of the heat kernel  But from the compactness of
But from the compactness of  ,
,  Therefore, the operator
Therefore, the operator 
is a Hilbert-Schmidt operator. It is thus in particular a compact operator.
Since  ,
,  is a product of two Hilbert-Schmidt operators. It is therefore a class trace operator and
is a product of two Hilbert-Schmidt operators. It is therefore a class trace operator and  We conclude then by applying the Chapman-Kolmogorov relation
We conclude then by applying the Chapman-Kolmogorov relation 
In this compact framework, we have the following theorem
Theorem: There exists a complete orthonormal basis  of
of  , consisting of eigenfunctions of
, consisting of eigenfunctions of  , with
, with 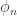 having an eigenvalue
having an eigenvalue 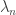 with finite multiplicity satisfying
with finite multiplicity satisfying  Moreover, for
Moreover, for 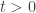 ,
,  ,
,  with convergence absolute and uniform for each
with convergence absolute and uniform for each 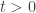 .
.
Proof: Let 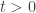 . From the Hilbert-Schmidt theorem for the non negative self adjoint compact operator
. From the Hilbert-Schmidt theorem for the non negative self adjoint compact operator  , there exists a complete orthonormal basis
, there exists a complete orthonormal basis  of
of  and a non increasing sequence
and a non increasing sequence  ,
,  such that
such that  The semigroup property
The semigroup property  implies first that for
implies first that for 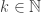 ,
, 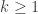 ,
,  The same result is then seen to hold for
The same result is then seen to hold for  ,
, 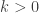 and finally for
and finally for  , due to the strong continuity of the semigroup. Since the map
, due to the strong continuity of the semigroup. Since the map  is decreasing, we deduce that
is decreasing, we deduce that  . Thus, there is a
. Thus, there is a  such that
such that  . As a conclusion, there exists a complete orthonormal basis
. As a conclusion, there exists a complete orthonormal basis  of $\mathbf{L}^2_\mu (\mathbb{M},\mathbb{R})$, and a sequence
of $\mathbf{L}^2_\mu (\mathbb{M},\mathbb{R})$, and a sequence 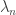 satisfying
satisfying  such that
such that  Since
Since  , we actually have
, we actually have 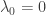 . Also, if
. Also, if  is such that
is such that  , it is straightforward that
, it is straightforward that  and that
and that  , so that thanks to Liouville theorem,
, so that thanks to Liouville theorem,  is a constant function. Therefore
is a constant function. Therefore  .
.
Since  , by differentiating as
, by differentiating as  in
in  , we obtain furthermore that
, we obtain furthermore that  and that
and that  . The family
. The family  forms an orthonormal basis of
forms an orthonormal basis of  . We therefore have a decomposition in
. We therefore have a decomposition in  ,
,  Since
Since  is the kernel of
is the kernel of  , it is then straightforward that for
, it is then straightforward that for  ,
,  and that
and that  . Therefore in
. Therefore in  ,
,  The continuity of
The continuity of  , together with the positivity of
, together with the positivity of  imply, via Mercer’s theorem that actually, the above series is absolutely and uniformly convergent for
imply, via Mercer’s theorem that actually, the above series is absolutely and uniformly convergent for 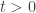

As we stressed it in the statement of the theorem, in the decomposition  the eigenvalue
the eigenvalue 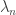 is repeated according to its multiplicity. It is often useful to rewrite this decomposition under the form
is repeated according to its multiplicity. It is often useful to rewrite this decomposition under the form  where the eigenvalue
where the eigenvalue 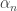 is not repeated, that is
is not repeated, that is  In this decomposition,
In this decomposition, 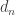 is the dimension of the eigenspace
is the dimension of the eigenspace 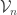 corresponding to the eigenvalue
corresponding to the eigenvalue 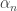 and
and  is an orthonormal basis of
is an orthonormal basis of 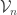 . If we denote,
. If we denote,  then
then  is called the reproducing kernel of the eigenspace
is called the reproducing kernel of the eigenspace 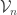 . It satisfies the following properties whose proofs are let to the reader:
. It satisfies the following properties whose proofs are let to the reader:
Proposition:
-
 does not depend on the choice of the basis
does not depend on the choice of the basis  ;
;
- If
 , then
, then  .
.
From the very definition of the reproducing kernels, we have 
The compactness of  also implies the convergence to equilibrium for the semigroup with an exponential rate.
also implies the convergence to equilibrium for the semigroup with an exponential rate.
Proposition: Let  , then uniformly on
, then uniformly on  , when
, when 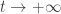 ,
, 
Proof: It is obvious from the previous proposition and from spectral theory that in  ,
,  converges to a constant function that we denote
converges to a constant function that we denote  . The convergence is also uniform, because for
. The convergence is also uniform, because for  ,
,




Moreover, for every 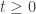 ,
,  . Therefore
. Therefore  Since
Since  is constant, we finally deduce the expected result
is constant, we finally deduce the expected result 


