Let  be a Hilbert space and let
be a Hilbert space and let  be a densely defined operator on a domain
be a densely defined operator on a domain  . We have the following basic definitions.
. We have the following basic definitions.
- The operator
 is said to be symmetric if for
is said to be symmetric if for  ,
,

- The operator
 is said to be non negative symmetric operator, if it is symmetric and if for
is said to be non negative symmetric operator, if it is symmetric and if for  ,
,

It is said to be non positive, if for  ,
,

The adjoint 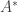 of
of  is the operator defined on the domain
is the operator defined on the domain 
and given through the Riesz representation theorem by the formula

where  . The operator
. The operator  is said to be self-adjoint if it is symmetric and if
is said to be self-adjoint if it is symmetric and if  .
.
Let us observe that, in general, the adjoint 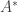 is not necessarily densely defined, however it is readily checked that if
is not necessarily densely defined, however it is readily checked that if  is a symmetric operator then, from Cauchy-Schwarz inequality,
is a symmetric operator then, from Cauchy-Schwarz inequality,  . Thus, if
. Thus, if  is symmetric, then
is symmetric, then 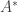 is densely defined.
is densely defined.
We have the following first criterion for self-adjointness which may be useful.
Lemma: Let  be a densely defined operator. Consider the graph of
be a densely defined operator. Consider the graph of  :
:

and the complex structure

Then, the operator  is self-adjoint if and only if
is self-adjoint if and only if

Proof: It is checked that for any densely defined operator 

and the conclusion follows from routine computations. 
The following result is often useful.
Lemma: Let  be an injective densely defined self-adjoint operator. Let us denote by
be an injective densely defined self-adjoint operator. Let us denote by 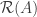 the range of
the range of  . The inverse operator
. The inverse operator  is a densely defined self-adjoint operator.
is a densely defined self-adjoint operator.
Proof: First, let us observe that

Therefore 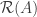 is dense in
is dense in  and $A^{-1}$ is densely defined. Now,
and $A^{-1}$ is densely defined. Now,





A major result in functional analysis is the spectral theorem.
Theorem: (Spectral theorem) Let  be a non negative self-adjoint operator on a separable Hilbert space
be a non negative self-adjoint operator on a separable Hilbert space  . There is a measure space
. There is a measure space  , a unitary map
, a unitary map  and a non negative real valued measurable function
and a non negative real valued measurable function  on
on 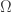 such that
such that  , for
, for  ,
,  . Moreover, given
. Moreover, given  ,
,  belongs to
belongs to  if only if
if only if  .
.
Definition: Let  be a non negative self-adjoint operator on
be a non negative self-adjoint operator on  . Let
. Let  be a Borel function. With the notations of the spectral theorem, one defines the operator
be a Borel function. With the notations of the spectral theorem, one defines the operator  by the requirement
by the requirement

with  .
.
Exercise: Show that if  is a non negative self-adjoint operator on
is a non negative self-adjoint operator on  and
and  is a bounded Borel function, then
is a bounded Borel function, then  is a bounded operator on
is a bounded operator on  .
.
As in the previous lecture, we have the following definition:
Definition: A strongly continuous self-adjoint contraction semigroup is a family of self-adjoint operators  everywhere defined on
everywhere defined on  such that:
such that:
- For
 ,
,  (semigroup property);
(semigroup property);
- For every
 ,
,  (strong continuity);
(strong continuity);
- For every
 and
and 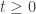 ,
,  (contraction property).
(contraction property).
Definition: A closed symmetric non negative bilinear form on  is a densely defined non negative quadratic form
is a densely defined non negative quadratic form  such that
such that  equipped with the norm
equipped with the norm  is a Hilbert space. If
is a Hilbert space. If 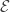 is a closed symmetric non negative bilinear form on
is a closed symmetric non negative bilinear form on  , one can define for
, one can define for  ,
,  .
.
One has the following theorems:
Theorem 1: Let  be a strongly continuous self-adjoint contraction semigroup on
be a strongly continuous self-adjoint contraction semigroup on  . Then its generator
. Then its generator  is a densely defined non positive self-adjoint operator on
is a densely defined non positive self-adjoint operator on  . Conversely, if
. Conversely, if  is a densely defined non positive self-adjoint operator on
is a densely defined non positive self-adjoint operator on  , then it is the generator a strongly continuous self-adjoint contraction semigroup on
, then it is the generator a strongly continuous self-adjoint contraction semigroup on  .
.
Proof: Let  be a strongly continuous self-adjoint contraction semigroup on
be a strongly continuous self-adjoint contraction semigroup on  with generator
with generator  . As we proved in the previous lecture, one has for
. As we proved in the previous lecture, one has for 

However, the operator  is seen to be self-adjoint, thus
is seen to be self-adjoint, thus  is. From previous lemma, we deduce that
is. From previous lemma, we deduce that  is self-adjoint, from which we deduce that
is self-adjoint, from which we deduce that  is self-adjoint (exercise !).
is self-adjoint (exercise !).
On the other hand, let  be a densely defined non positive self-adjoint operator on
be a densely defined non positive self-adjoint operator on  . From spectral theorem, there is a measure space
. From spectral theorem, there is a measure space  , a unitary map
, a unitary map  and a non negative real valued measurable function
and a non negative real valued measurable function  on
on 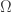 such that
such that

for  ,
,  . We define then
. We define then  such that
such that

and let as an exercise the proof that  is a strongly continuous self-adjoint contraction semigroup on
is a strongly continuous self-adjoint contraction semigroup on  with generator
with generator  .
. 
Theorem 2: Let  be a strongly continuous self-adjoint contraction semigroup on
be a strongly continuous self-adjoint contraction semigroup on  . One can define a closed symmetric non negative bilinear form on
. One can define a closed symmetric non negative bilinear form on  by
by

The domain  of this form is the set of
of this form is the set of  ‘s for which the limit exists.
‘s for which the limit exists.
Proof: Let  be the generator of the semigroup
be the generator of the semigroup  . We use spectral theorem to represent
. We use spectral theorem to represent  as
as

so that

We then note that for every  ,
,

This proves that for every  , the map
, the map  is non increasing. Therefore, the limit
is non increasing. Therefore, the limit  exists if and only if
exists if and only if  , which is equivalent to the fact that
, which is equivalent to the fact that  . In which case we have
. In which case we have

Since  is a densely defined self-adjoint operator, the quadratic form
is a densely defined self-adjoint operator, the quadratic form

is closed and densely defined on  .
.
Theorem 3: If 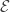 is a closed symmetric non negative bilinear form on
is a closed symmetric non negative bilinear form on  . There exists a unique densely defined non positive self-adjoint operator
. There exists a unique densely defined non positive self-adjoint operator  on
on  defined by
defined by


The operator  is called the generator of
is called the generator of 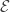 . Conversely, if
. Conversely, if  is a densely defined non positive self-adjoint operator on
is a densely defined non positive self-adjoint operator on  , one can define a closed symmetric non negative bilinear form
, one can define a closed symmetric non negative bilinear form 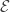 on
on  by
by

Proof: Let 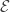 be a closed symmetric non negative bilinear form on
be a closed symmetric non negative bilinear form on  . As usual, we denote by
. As usual, we denote by  the domain of
the domain of 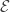 . We note that for
. We note that for  ,
,  equipped with the norm
equipped with the norm  is a Hilbert space because
is a Hilbert space because  is closed. From the Riesz representation theorem, there exists then a linear operator
is closed. From the Riesz representation theorem, there exists then a linear operator  such that for every
such that for every 

From the definition, the following properties are then easily checked:
1) 
2) For every  ,
,  ;
;
3)  ;
;
4) For every  ,
,  .
.
We then claim that  is invertible. Indeed, if
is invertible. Indeed, if  , then for
, then for  , one has from 3,
, one has from 3,  . Therefore
. Therefore  . Denote then
. Denote then

and  is the range of
is the range of  . It is straightforward to check that
. It is straightforward to check that  does not depend on
does not depend on  . The operator
. The operator  is a densely defined self-adjoint operator that satisfies the properties stated in the theorem (Exercise !).
is a densely defined self-adjoint operator that satisfies the properties stated in the theorem (Exercise !). 
As a conclusion one has bijections between the set of non positive self-adjoint operators, the set of closed symmetric non negative bilinear form and the set of strongly continuous self-adjoint contraction semigroups. This is the golden triangle of the theory of heat semigroups on Hilbert spaces !
Let  be a densely defined operator. A densely defined operator
be a densely defined operator. A densely defined operator  is called an extension of
is called an extension of  if
if  and for every
and for every  ,
,  .
.
Theorem: (Friedrichs extension) Let  be a densely defined non positive symmetric operator on
be a densely defined non positive symmetric operator on  . There exists at least one self-adjoint extension of
. There exists at least one self-adjoint extension of  .
.
Proof: On  , let us consider the following norm
, let us consider the following norm

By completing  with respect to this norm, we get an abstract Hilbert space
with respect to this norm, we get an abstract Hilbert space  . Since for
. Since for  ,
,  , the injection map
, the injection map  is continuous and it may therefore be extended into a continuous map
is continuous and it may therefore be extended into a continuous map  . Let us show that
. Let us show that  is injective so that
is injective so that 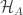 may be identified with a subspace of
may be identified with a subspace of  . So, let
. So, let  such that
such that  . We can find a sequence
. We can find a sequence  , such that
, such that  and
and  . We have then
. We have then

thus 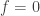 and
and  is injective. Therefore,
is injective. Therefore, 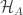 may be identified with a subspace of
may be identified with a subspace of  . Since
. Since  , one has that
, one has that 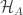 is dense in
is dense in  . We consider now the quadratic form on $\mathcal{H}$ defined by
. We consider now the quadratic form on $\mathcal{H}$ defined by

It is closed because  is a Hilbert space. The generator of this quadratic form is then a self-adjoint extension of
is a Hilbert space. The generator of this quadratic form is then a self-adjoint extension of  .
.

In general self-adjoint extensions of a given symmetric operator are not unique. The operator constructed in the proof above is called the Friedrichs extension of  . It is the minimal self-adjoint extension of
. It is the minimal self-adjoint extension of  .
.
Definition: Let  be a densely defined non positive symmetric operator on
be a densely defined non positive symmetric operator on  . We say that
. We say that  is essentially self-adjoint if it admits a unique self-adjoint extension.
is essentially self-adjoint if it admits a unique self-adjoint extension.
We have the following criterion for essential self-adjointness.
Exercise: Let  be a densely defined non positive symmetric operator on
be a densely defined non positive symmetric operator on  . If for some
. If for some  ,
,

then the operator  is essentially self-adjoint.
is essentially self-adjoint.
denote the number of red balls chosen.
?
?
be the sum.
.

